SLIM2D is used in shallow-water environments where wind and tides are sufficient to keep the water column rather well mixed. It solves the depth-averaged shallow water equations for the surface elevation and the horizontal velocity. When the horizontal flow is mainly unidirectional such as for a well-mixed river, the shallow water equations can be averaged over the section leading to the 1D section-averaged shallow-water equations. SLIM1D consists of linear river segments where variable river width and cross-section are taken into account. River segments can be joined to model a river network with accurate computation of bifurcation by the means of a Riemann solver.
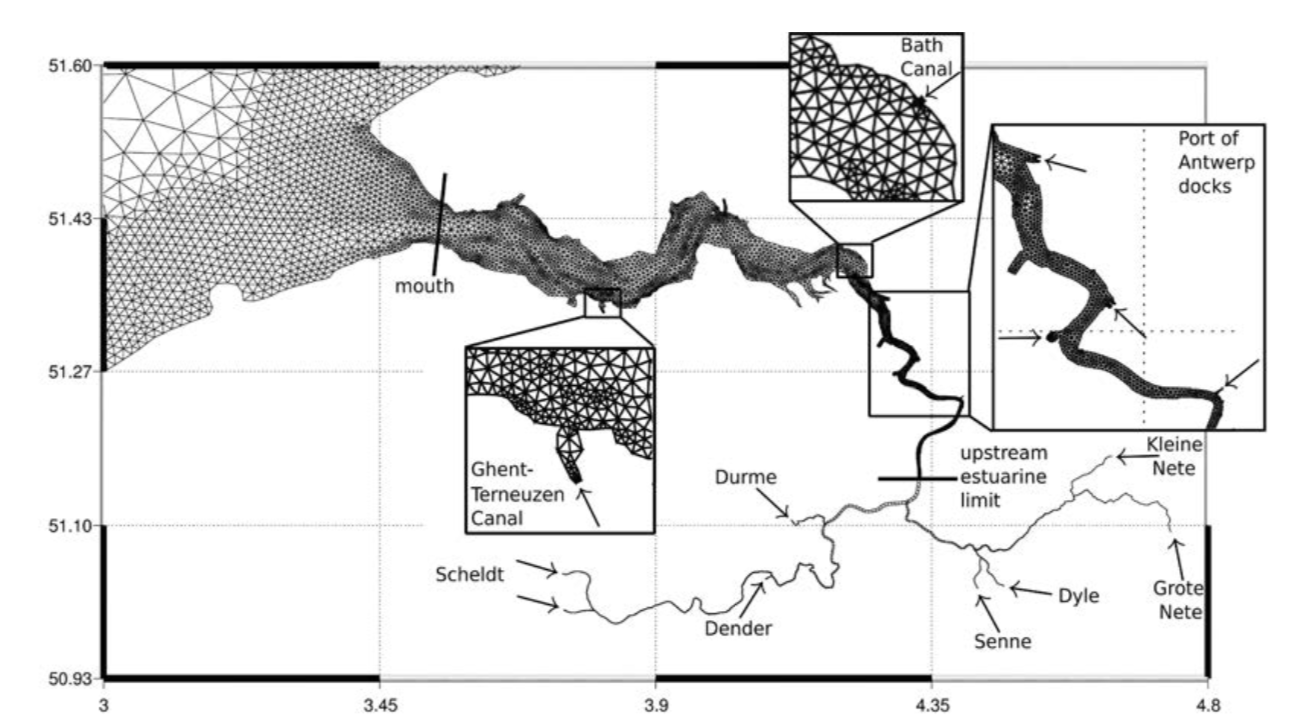
2D-1D mesh of the Schledt river, estuary and its tributaries. SLIM2D is used in the estuary and coastal sea. Upstream of the estuary, the mesh becomes one-dimensional in the fresh tidal river network and ends at the limit of the tidal dominance. The arrows indicated the locations where freshwater discharges are imposed. SLIM solves the model equations on an unstructured mesh with the Discontinuous Galerkin finite element method. This approach provides an optimal degree of flexibility both geometrically and functionally as it can accurately represent complex topographies and also model solutions with sharp gradients. Unlike more standard numerical methods, such as finite volumes, it introduces a minimal amount of numerical dissipation and thus preserves small-scale flow features such as recirculation eddies. The model equations can be forced by wind, tides, river discharges and large-scale currents from a global ocean model.
Currents as modelled with SLIM2D in the Great Barrier Reef. The use of an unstructured mesh with a 250m resolution and the Discontinuous Galerkin method allows us to simulate small-scale flow features such as recirculation eddies. Most coastal areas are significantly influenced by tides. When approaching the coast, the tidal signal tends to amplify, especially in funnel-shaped embayments where the tidal range may reach considerable magnitudes. Combined with the fact that many estuaries and embayments also feature gradually sloping bathymetry, the total area submerged under water may vary significantly during the tidal cycle. To tackle this issues, SLIM2D is equipped with a wetting-drying algorithm that allows it to handle dry areas. The algorithm is based on an implicit time-stepping that combines computational efficiency with local mass conservation. The video below shows the water transport in the Columbia River estuary as modeled by SLIM2D. Dry tidal flats are clearly visible at low tide.
VIDEO
To learn more…
778265
SLIM2D
1
apa
50
date
desc
6963
https://www.slim-ocean.be/wp-content/plugins/zotpress/
%7B%22status%22%3A%22success%22%2C%22updateneeded%22%3Afalse%2C%22instance%22%3Afalse%2C%22meta%22%3A%7B%22request_last%22%3A0%2C%22request_next%22%3A0%2C%22used_cache%22%3Atrue%7D%2C%22data%22%3A%5B%7B%22key%22%3A%22N7DF8AKK%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Scherpereel%20et%20al.%22%2C%22parsedDate%22%3A%222025%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BScherpereel%2C%20C.%2C%20Alosairi%2C%20Y.%2C%20Lambrechts%2C%20J.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282025%29.%20Hydrodynamic%20impacts%20of%20bridge%20construction%20and%20land%20reclamation%20on%20water%20residence%20time%20and%20flushing%20processes%20in%20Kuwait%20Bay.%20%26lt%3Bi%26gt%3BMarine%20Pollution%20Bulletin%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B214%26lt%3B%5C%2Fi%26gt%3B%2C%20117716.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.marpolbul.2025.117716%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.marpolbul.2025.117716%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hydrodynamic%20impacts%20of%20bridge%20construction%20and%20land%20reclamation%20on%20water%20residence%20time%20and%20flushing%20processes%20in%20Kuwait%20Bay%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Colin%22%2C%22lastName%22%3A%22Scherpereel%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Yousef%22%2C%22lastName%22%3A%22Alosairi%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22Over%20the%20past%20few%20decades%2C%20Kuwait%20Bay%20has%20experienced%20significant%20water%20quality%20decline%20due%20to%20growing%20anthropogenic%20pressures%2C%20including%20oil%20and%20gas%20extraction%20and%20extensive%20coastal%20developments%2C%20leading%20to%20severe%20eutrophication%20and%20marine%20life%20mortality.%20Additionally%2C%20the%20recent%20construction%20of%20a%2036%20km-long%20causeway%20across%20the%20Bay%20and%20related%20land%20reclamation%20projects%20has%20disrupted%20the%20Bay%26%23039%3Bs%20natural%20flushing%20processes%2C%20allowing%20pollutants%20and%20excess%20nutrients%20to%20accumulate%20more%20readily.%20However%2C%20the%20impact%20of%20these%20new%20infrastructures%20on%20the%20Bay%26%23039%3Bs%20circulation%20patterns%20and%20water%20renewal%20capacity%20remains%20unquantified.%20Here%2C%20we%20use%20the%20multi-scale%20ocean%20model%20SLIM%20to%20simulate%20the%20fine-scale%20flow%20patterns%20in%20Kuwait%20Bay%20and%20evaluate%20water%20residence%20time%20distribution%2C%20focusing%20on%20its%20spatial%20and%20seasonal%20variability.%20By%20further%20comparing%20pre-%20and%20post-construction%20scenarios%2C%20we%20quantify%20the%20causeway%26%23039%3Bs%20influence%20on%20Kuwait%20Bay%26%23039%3Bs%20hydrodynamics%20and%20flushing%20properties.%20We%20find%20a%20complete%20renewal%20of%20the%20Bay%20within%20150%5Cu2013320%20days%2C%20driven%20by%20significant%20spatial%20and%20seasonal%20variations%20in%20water%20residence%20time%2C%20largely%20influenced%20by%20the%20prevailing%20winds%20and%20strong%20tidal%20flows%20interacting%20with%20the%20Bay%26%23039%3Bs%20shallow%20depths.%20The%20introduction%20of%20the%20artificial%20structures%20extends%20the%20average%20residence%20time%20by%20only%201.29%20days%20%28%2B3.49%20%25%29%2C%20but%20with%20significant%20local%20variations%20ranging%20from%2066%20to%20%2B56%20days%2C%20underlining%20the%20causeway%26%23039%3Bs%20role%20as%20a%20physical%20barrier%2C%20and%20amplifying%20the%20risks%20of%20water%20quality%20degradation%20in%20some%20regions.%20From%20a%20broader%20perspective%2C%20our%20findings%20highlight%20the%20large-scale%20impact%20of%20fine-scale%20hydrodynamic%20changes%20in%20a%20semi-enclosed%20coastal%20system%20on%20its%20flushing%20processes%20and%20water%20quality.%22%2C%22date%22%3A%2205%5C%2F2025%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.marpolbul.2025.117716%22%2C%22ISSN%22%3A%220025326X%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0025326X25001912%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222025-03-03T08%3A06%3A46Z%22%7D%7D%2C%7B%22key%22%3A%229GBCLPET%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Hirsh%20et%20al.%22%2C%22parsedDate%22%3A%222025%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BHirsh%2C%20H.%20K.%2C%20Oliver%2C%20T.%20A.%2C%20Dobbelaere%2C%20T.%2C%20Palacio-Castro%2C%20A.%20M.%2C%20Barkley%2C%20H.%20C.%2C%20Webb%2C%20A.%20E.%2C%20Hanert%2C%20E.%2C%20%26amp%3B%20Enochs%2C%20I.%20C.%20%282025%29.%20Statistical%20Prediction%20of%20In%20Situ%20Coral%20Reef%20Carbonate%20Dynamics%20Using%20Endmember%20Chemistry%2C%20Hydrodynamic%20Models%2C%20And%20Benthic%20Composition.%20%26lt%3Bi%26gt%3BAquatic%20Geochemistry%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B31%26lt%3B%5C%2Fi%26gt%3B%281%29%2C%204.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10498-025-09438-x%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10498-025-09438-x%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Statistical%20Prediction%20of%20In%20Situ%20Coral%20Reef%20Carbonate%20Dynamics%20Using%20Endmember%20Chemistry%2C%20Hydrodynamic%20Models%2C%20And%20Benthic%20Composition%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Heidi%20K.%22%2C%22lastName%22%3A%22Hirsh%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%20A.%22%2C%22lastName%22%3A%22Oliver%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Dobbelaere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ana%20M.%22%2C%22lastName%22%3A%22Palacio-Castro%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Hannah%20C.%22%2C%22lastName%22%3A%22Barkley%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Alice%20E.%22%2C%22lastName%22%3A%22Webb%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ian%20C.%22%2C%22lastName%22%3A%22Enochs%22%7D%5D%2C%22abstractNote%22%3A%22In%20the%20face%20of%20rapidly%20compounding%20climate%20change%20impacts%2C%20including%20ocean%20acidification%20%28OA%29%2C%20it%20is%20critical%20to%20understand%20present-day%20stress%20exposure%20and%20to%20anticipate%20the%20biogeochemical%20conditions%20experienced%20by%20vulnerable%20ecosystems%20like%20coral%20reefs.%20To%20meaningfully%20predict%20nearshore%20carbonate%20chemistry%2C%20we%20must%20account%20for%20the%20complexity%20of%20the%20local%20benthic%20community%2C%20as%20well%20as%20connectivity%20between%20habitats%20and%20relevant%20endmember%20carbonate%20chemistry.%20Here%2C%20we%20adopt%20a%20system-scale%20approach%20to%20predict%20site-scale%20effects%20of%20benthic%20metabolism%20on%20the%20carbonate%20system%20of%20the%20Florida%20Reef%20Tract%20%28FRT%29.%20We%20utilize%20bimonthly%20carbonate%20chemistry%20data%20from%20ten%20cross-shelf%20transects%20spanning%20250%20km%20of%20the%20FRT%20to%20model%20changes%20in%20dissolved%20inorganic%20carbon%20%28DIC%29%20and%20total%20alkalinity%20%28TA%29.%20Benthic%20habitat%20maps%20were%20used%20to%20broadly%20classify%20communities%20known%20to%20impact%20carbonate%20chemistry.%20A%20SLIM%202D%20hydrodynamic%20model%20with%20mesh%20resolution%20reaching%20100%20m%20over%20reefs%20and%20along%20the%20coastline%20was%20used%20to%20determine%20the%20relevant%20water%20mass%20histories%20and%20identify%20the%20upstream%20benthic%20communities%20shaping%20local%20carbonate%20chemistry.%20These%20historical%20metabolic%20footprints%2C%20or%20%5Cu201cflowsheds%5Cu201d%2C%20were%20used%20to%20build%20predictive%20models%20of%20the%20change%20in%20DIC%20and%20TA%20at%20each%20station.%20The%20best%20predictive%20models%20included%20the%20chemical%20impacts%20of%20benthic%20ecosystem%20metabolism%2C%20as%20defined%20by%20water%20mass%20trajectories%2C%20weighted%20endmember%20chemistry%2C%20volume%2C%20time%2C%20and%20other%20environmental%20parameters%20%28light%2C%20temperature%2C%20salinity%2C%20chlorophyll-a%2C%20and%20nitrate%29.%20Considering%20water%20mass%20for%205%20days%20prior%20to%20sample%20collection%20yielded%20the%20highest%20model%20skill.%22%2C%22date%22%3A%2202%5C%2F2025%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs10498-025-09438-x%22%2C%22ISSN%22%3A%221380-6165%2C%201573-1421%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs10498-025-09438-x%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222025-02-26T11%3A44%3A54Z%22%7D%7D%2C%7B%22key%22%3A%22IZMKRZRG%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Dobbelaere%20et%20al.%22%2C%22parsedDate%22%3A%222024%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BDobbelaere%2C%20T.%2C%20Holstein%2C%20D.%20M.%2C%20Gramer%2C%20L.%20J.%2C%20McEachron%2C%20L.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282024%29.%20Investigating%20the%20link%20between%20the%20Port%20of%20Miami%20dredging%20and%20the%20onset%20of%20the%20stony%20coral%20tissue%20loss%20disease%20epidemics.%20%26lt%3Bi%26gt%3BMarine%20Pollution%20Bulletin%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B207%26lt%3B%5C%2Fi%26gt%3B%2C%20116886.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.marpolbul.2024.116886%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.marpolbul.2024.116886%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Investigating%20the%20link%20between%20the%20Port%20of%20Miami%20dredging%20and%20the%20onset%20of%20the%20stony%20coral%20tissue%20loss%20disease%20epidemics%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Dobbelaere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Daniel%20M.%22%2C%22lastName%22%3A%22Holstein%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Lewis%20J.%22%2C%22lastName%22%3A%22Gramer%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Lucas%22%2C%22lastName%22%3A%22McEachron%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22Since%202014%2C%20the%20stony%20coral%20tissue%20loss%20disease%20%28SCTLD%29%20has%20been%20decimating%20corals%20in%20the%20Caribbean.%20Although%20the%20trigger%20of%20this%20outbreak%20remains%20elusive%2C%20evidence%20suggests%20waterborne%20sediment-mediated%20disease%20transmission.%20The%20outbreak%20reportedly%20initiated%20in%20September%202014%20at%20a%20reef%20site%20off%20Virginia%20Key%20%28VKR%29%2C%20during%20extensive%20dredging%20operations%20at%20the%20Port%20of%20Miami.%20Here%20we%20use%20a%20high-resolution%20ocean%20model%20to%20identify%20the%20potential%20driver%20of%20the%20outbreak%20by%20simulating%20the%20dispersal%20of%20dredged%20sediments%2C%20wastewater%20plumes%20and%20disease%20agents.%20Our%20results%20suggest%20that%20VKR%20could%20have%20been%20impacted%20by%20fine%20sediments%20produced%20by%20dredging%20operations%2C%20especially%20those%20involving%20non-conventional%20rock-chopping%20techniques.%20Wastewater%20contamination%20was%20unlikely.%20Additionally%2C%20our%20connectivity%20analysis%20indicates%20potential%20disease%20transmission%20from%20other%20affected%20reefs%20to%20VKR.%20Our%20results%20therefore%20suggest%20that%20dredging%20operations%20might%20be%20responsible%20for%20the%20onset%20of%20the%20epidemics.%20This%20underscores%20the%20need%20for%20stricter%20operational%20guidelines%20in%20future%20dredging%20projects.%22%2C%22date%22%3A%2210%5C%2F2024%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.marpolbul.2024.116886%22%2C%22ISSN%22%3A%220025326X%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0025326X24008634%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222024-09-02T09%3A12%3A35Z%22%7D%7D%2C%7B%22key%22%3A%227RAKJ2F9%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Dobbelaere%20et%20al.%22%2C%22parsedDate%22%3A%222024%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BDobbelaere%2C%20T.%2C%20Dekens%2C%20A.%2C%20Saint%26%23x2010%3BAmand%2C%20A.%2C%20Alaerts%2C%20L.%2C%20Holstein%2C%20D.%20M.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282024%29.%20Hurricanes%20enhance%20coral%20connectivity%20but%20also%20superspread%20coral%20diseases.%20%26lt%3Bi%26gt%3BGlobal%20Change%20Biology%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B30%26lt%3B%5C%2Fi%26gt%3B%286%29%2C%20e17382.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1111%5C%2Fgcb.17382%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1111%5C%2Fgcb.17382%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Hurricanes%20enhance%20coral%20connectivity%20but%20also%20superspread%20coral%20diseases%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Dobbelaere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Apolline%22%2C%22lastName%22%3A%22Dekens%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Antoine%22%2C%22lastName%22%3A%22Saint%5Cu2010Amand%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Lauranne%22%2C%22lastName%22%3A%22Alaerts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Daniel%20M.%22%2C%22lastName%22%3A%22Holstein%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22Climate%20change%20poses%20an%20existential%20threat%20to%20coral%20reefs.%20A%20warmer%20and%20more%20acidic%20ocean%20weakens%20coral%20ecosystems%20and%20increases%20the%20intensity%20of%20hurricanes.%20The%20wind%5Cu2013wave%5Cu2013current%20interactions%20during%20a%20hurricane%20deeply%20change%20the%20ocean%20circulation%20patterns%20and%20hence%20potentially%20affect%20the%20dispersal%20of%20coral%20larvae%20and%20coral%20disease%20agents.%20Here%2C%20we%20modeled%20the%20impact%20of%20major%20hurricane%20Irma%20%28September%202017%29%20on%20coral%20larval%20and%20stony%20coral%20tissue%20loss%20disease%20%28SCTLD%29%20connectivity%20in%20Florida%26%23039%3Bs%20Coral%20Reef.%20We%20coupled%20high-%5Cu00adresolution%20coastal%20ocean%20circulation%20and%20wave%20models%20to%20simulate%20the%20dispersal%20of%20virtual%20coral%20larvae%20and%20disease%20agents%20between%20thousands%20of%20reefs.%20While%20being%20a%20brief%20event%2C%20our%20results%20suggest%20the%20passage%20of%20hurricane%20Irma%20strongly%20increased%20the%20probability%20of%20long-%5Cu00addistance%20exchanges%20while%20reducing%20larval%20supply.%20It%20created%20new%20connections%20that%20could%20promote%20coral%20resilience%20but%20also%20probably%20accelerated%20the%20spread%20of%20SCTLD%20by%20about%20a%20month.%20As%20they%20become%20more%20intense%2C%20hurricanes%26%23039%3B%20double-%5Cu00adedged%20effect%20will%20become%20increasingly%20pronounced%2C%20contributing%20to%20increased%20variability%20in%20transport%20patterns%20and%20an%20accelerated%20rate%20of%20change%20within%20coral%20reef%20ecosystems.%22%2C%22date%22%3A%2206%5C%2F2024%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1111%5C%2Fgcb.17382%22%2C%22ISSN%22%3A%221354-1013%2C%201365-2486%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fonlinelibrary.wiley.com%5C%2Fdoi%5C%2F10.1111%5C%2Fgcb.17382%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222024-06-26T06%3A17%3A17Z%22%7D%7D%2C%7B%22key%22%3A%22MW6CBVLC%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Faryuni%20et%20al.%22%2C%22parsedDate%22%3A%222024%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BFaryuni%2C%20I.%20D.%2C%20Saint-Amand%2C%20A.%2C%20Dobbelaere%2C%20T.%2C%20Umar%2C%20W.%2C%20Jompa%2C%20J.%2C%20Moore%2C%20A.%20M.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282024%29.%20Assessing%20coral%20reef%20conservation%20planning%20in%20Wakatobi%20National%20Park%20%28Indonesia%29%20from%20larval%20connectivity%20networks.%20%26lt%3Bi%26gt%3BCoral%20Reefs%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B43%26lt%3B%5C%2Fi%26gt%3B%281%29%2C%2019%26%23x2013%3B33.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs00338-023-02443-y%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs00338-023-02443-y%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Assessing%20coral%20reef%20conservation%20planning%20in%20Wakatobi%20National%20Park%20%28Indonesia%29%20from%20larval%20connectivity%20networks%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Irfana%20Diah%22%2C%22lastName%22%3A%22Faryuni%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Antoine%22%2C%22lastName%22%3A%22Saint-Amand%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Dobbelaere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Widyastuti%22%2C%22lastName%22%3A%22Umar%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jamaluddin%22%2C%22lastName%22%3A%22Jompa%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Abigail%20Mary%22%2C%22lastName%22%3A%22Moore%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%2202%5C%2F2024%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs00338-023-02443-y%22%2C%22ISSN%22%3A%220722-4028%2C%201432-0975%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs00338-023-02443-y%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222024-06-26T07%3A09%3A10Z%22%7D%7D%2C%7B%22key%22%3A%22NHMPBUXX%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Lecart%20et%20al.%22%2C%22parsedDate%22%3A%222024%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BLecart%2C%20M.%2C%20Dobbelaere%2C%20T.%2C%20Alaerts%2C%20L.%2C%20Randresihaja%2C%20N.%20R.%2C%20Mohammed%2C%20A.%20V.%2C%20Vethamony%2C%20P.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282024%29.%20Land%20reclamation%20and%20its%20consequences%3A%20A%2040-year%20analysis%20of%20water%20residence%20time%20in%20Doha%20Bay%2C%20Qatar.%20%26lt%3Bi%26gt%3BPLOS%20ONE%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B19%26lt%3B%5C%2Fi%26gt%3B%281%29%2C%20e0296715.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1371%5C%2Fjournal.pone.0296715%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1371%5C%2Fjournal.pone.0296715%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Land%20reclamation%20and%20its%20consequences%3A%20A%2040-year%20analysis%20of%20water%20residence%20time%20in%20Doha%20Bay%2C%20Qatar%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Mathieu%22%2C%22lastName%22%3A%22Lecart%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Dobbelaere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Lauranne%22%2C%22lastName%22%3A%22Alaerts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ny%20Riana%22%2C%22lastName%22%3A%22Randresihaja%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Aboobacker%20Valliyil%22%2C%22lastName%22%3A%22Mohammed%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ponnumony%22%2C%22lastName%22%3A%22Vethamony%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222024%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1371%5C%2Fjournal.pone.0296715%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222024-06-26T07%3A27%3A33Z%22%7D%7D%2C%7B%22key%22%3A%22Z73QS8B5%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Saint-Amand%20et%20al.%22%2C%22parsedDate%22%3A%222023-06-09%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BSaint-Amand%2C%20A.%2C%20Lambrechts%2C%20J.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282023%29.%20Biophysical%20models%20resolution%20affects%20coral%20connectivity%20estimates.%20%26lt%3Bi%26gt%3BScientific%20Reports%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B13%26lt%3B%5C%2Fi%26gt%3B%281%29%2C%209414.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1038%5C%2Fs41598-023-36158-5%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1038%5C%2Fs41598-023-36158-5%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Biophysical%20models%20resolution%20affects%20coral%20connectivity%20estimates%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Antoine%22%2C%22lastName%22%3A%22Saint-Amand%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22Abstract%5Cn%20%20%20%20%20%20%20%20%20%20%20%20Estimating%20connectivity%20between%20coral%20reefs%20is%20essential%20to%20inform%20reef%20conservation%20and%20restoration.%20Given%20the%20vastness%20of%20coral%20reef%20ecosystems%2C%20connectivity%20can%20only%20be%20simulated%20with%20biophysical%20models%20whose%20spatial%20resolution%20is%20often%20coarser%20than%20the%20reef%20scale.%20Here%2C%20we%20assess%20the%20impact%20of%20biophysical%20models%20resolution%20on%20connectivity%20estimates%20by%20comparing%20the%20outputs%20of%20five%20different%20setups%20of%20the%20same%20model%20with%20resolutions%20ranging%20from%20250%5Cu00a0m%20to%204%5Cu00a0km.%20We%20show%20that%20increasing%20the%20model%20resolution%20around%20reefs%20yields%20more%20complex%20and%20less%20directional%20dispersal%20patterns.%20With%20a%20fine-resolution%20model%2C%20connectivity%20graphs%20have%20more%20connections%20but%20of%20weaker%20strength.%20The%20resulting%20community%20structure%20therefore%20shows%20larger%20clusters%20of%20well-connected%20reefs.%20Virtual%20larvae%20also%20tend%20to%20stay%20longer%20close%20to%20their%20source%20reef%20with%20a%20fine-resolution%20model%2C%20leading%20to%20an%20increased%20local%20retention%20and%20self-recruitment%20for%20species%20with%20a%20short%20pre-competency%20period.%20Overall%2C%20only%20about%20half%20of%20the%20reefs%20with%20the%20largest%20connectivity%20indicator%20values%20are%20similar%20for%20the%20finest%20and%20coarsest%20resolution%20models.%20Our%20results%20suggest%20that%20reef%20management%20recommendations%20should%20only%20be%20made%20at%20scales%20coarser%20than%20the%20model%20resolution.%20Reef-scale%20recommendations%20can%20hence%20only%20be%20made%20with%20models%20not%20exceeding%20about%20500%5Cu00a0m%20resolution.%22%2C%22date%22%3A%222023-06-09%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1038%5C%2Fs41598-023-36158-5%22%2C%22ISSN%22%3A%222045-2322%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.nature.com%5C%2Farticles%5C%2Fs41598-023-36158-5%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-06-14T06%3A42%3A46Z%22%7D%7D%2C%7B%22key%22%3A%22V6TLSQ66%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Purkis%20et%20al.%22%2C%22parsedDate%22%3A%222023-03-31%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BPurkis%2C%20S.%20J.%2C%20Oehlert%2C%20A.%20M.%2C%20Dobbelaere%2C%20T.%2C%20Hanert%2C%20E.%2C%20%26amp%3B%20Harris%2C%20P.%20%28Mitch%29.%20%282023%29.%20Always%20a%20White%20Christmas%20in%20the%20Bahamas%3A%20temperature%20and%20hydrodynamics%20localize%20winter%20mud%20production%20on%20Great%20Bahama%20Bank.%20%26lt%3Bi%26gt%3BJournal%20of%20Sedimentary%20Research%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B93%26lt%3B%5C%2Fi%26gt%3B%283%29%2C%20145%26%23x2013%3B160.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.2110%5C%2Fjsr.2022.066%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.2110%5C%2Fjsr.2022.066%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Always%20a%20White%20Christmas%20in%20the%20Bahamas%3A%20temperature%20and%20hydrodynamics%20localize%20winter%20mud%20production%20on%20Great%20Bahama%20Bank%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sam%20J.%22%2C%22lastName%22%3A%22Purkis%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Amanda%20M.%22%2C%22lastName%22%3A%22Oehlert%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Dobbelaere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Paul%20%28Mitch%29%22%2C%22lastName%22%3A%22Harris%22%7D%5D%2C%22abstractNote%22%3A%22Whitings%2C%20or%20occurrences%20of%20%5Cufb01ne-grained%20carbonate%20in%20the%20water%20column%2C%20have%20been%20observed%20in%20modern%20environments%20with%20salinities%20ranging%20from%20fresh%20to%20marine%20conditions%2C%20and%20thick%20deposits%20of%20lime%20mud%20are%20described%20throughout%20the%20geological%20record.%20Despite%20their%20ubiquity%2C%20the%20trigger%20for%20whitings%20has%20been%20debated%20for%20more%20than%20eighty%20years.%20Satellite%20data%20reveal%20that%20most%20whitings%20are%20restricted%20to%20the%20northwestern%20part%20of%20Great%20Bahama%20Bank%20%28GBB%29%20which%20occupies%20%2C%2010%25%20of%20the%20platform%20area.%20Even%20here%2C%20whitings%20are%20further%20focused.%20More%20than%2035%25%20of%20them%20occur%20in%20a%20zone%20which%20occupies%20just%201%25%20of%20the%20platform.%20We%20propose%20a%20three-step%20process%20for%20the%20existence%20of%20this%20zone%20of%20peak%20whitings%20and%20why%20the%20whitings%20in%20it%20are%20both%20more%20frequent%20and%20larger%20in%20winter%20than%20summer.%20First%2C%20the%20temperature%20differential%20between%20on-%20and%20off-platform%20waters%20is%20highest%20in%20the%20winter%2C%20setting%20up%20a%20disparity%20between%20dissolved%20CO2%20concentrations%20in%20the%20two%20water%20masses.%20Second%2C%20hydrodynamic%20mixing%20of%20these%20two%20water%20masses%20increases%20the%20degree%20of%20aragonite%20saturation%20of%20the%20platform-top%20waters%2C%20as%20colder%20on-platform%20waters%20with%20theoretically%20higher%20concentrations%20of%20dissolved%20gases%20are%20warmed%20via%20mixing%20with%20the%20warmer%20off-platform%20waters.%20Finally%2C%20spatial%20heterogeneity%20in%20the%20degree%20of%20aragonite%20saturation%20is%20higher%20in%20the%20winter%2C%20and%20the%20zone%20of%20peak%20whitings%20is%20situated%20in%20an%20area%20of%20locally%20enhanced%20saturation%20state.%20Hydrodynamic%20simulation%20suggests%20that%20the%20whitings%20zone%20is%20located%20by%20tidal%20in%5Cufb02ow%20of%20off-platform%20waters%20across%20the%20western%20margin%20of%20GBB%2C%20as%20well%20as%20in%5Cufb02ow%20from%20the%20Tongue%20of%20the%20Ocean%20to%20the%20north%20of%20Andros%20Island.%20Despite%20thermodynamic%20forcing%20mechanisms%20that%20predict%20higher%20frequency%20of%20whitings%20in%20the%20summer%2C%20the%20environmental%2C%20hydrodynamic%2C%20geochemical%2C%20and%20kinetic%20conditions%20in%20the%20whitings%20zone%20appear%20to%20support%20the%20Goldilocks%20con%5Cufb01guration%20that%20enhances%20the%20formation%20of%20wintertime%20whitings%20on%20Great%20Bahama%20Bank.%20This%20phenomenon%20has%20implications%20for%20the%20interpretation%20of%20whitings%20mud%20in%20the%20geological%20record%2C%20including%20the%20geochemical%20signatures%20within%20it.%22%2C%22date%22%3A%222023-03-31%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.2110%5C%2Fjsr.2022.066%22%2C%22ISSN%22%3A%221938-3681%2C%201527-1404%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fpubs.geoscienceworld.org%5C%2Fjsedres%5C%2Farticle%5C%2F93%5C%2F3%5C%2F145%5C%2F620896%5C%2FAlways-a-White-Christmas-in-the-Bahamas%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-03-12T19%3A10%3A21Z%22%7D%7D%2C%7B%22key%22%3A%22AEK348B9%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22King%20et%20al.%22%2C%22parsedDate%22%3A%222023-01-17%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BKing%2C%20S.%2C%20Saint-Amand%2C%20A.%2C%20Walker%2C%20B.%20K.%2C%20Hanert%2C%20E.%2C%20%26amp%3B%20Figueiredo%2C%20J.%20%282023%29.%20Larval%20dispersal%20patterns%20and%20connectivity%20of%20Acropora%20on%20Florida%26%23x2019%3Bs%20Coral%20Reef%20and%20its%20implications%20for%20restoration.%20%26lt%3Bi%26gt%3BFrontiers%20in%20Marine%20Science%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B9%26lt%3B%5C%2Fi%26gt%3B%2C%201038463.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.3389%5C%2Ffmars.2022.1038463%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.3389%5C%2Ffmars.2022.1038463%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Larval%20dispersal%20patterns%20and%20connectivity%20of%20Acropora%20on%20Florida%5Cu2019s%20Coral%20Reef%20and%20its%20implications%20for%20restoration%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Samantha%22%2C%22lastName%22%3A%22King%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Antoine%22%2C%22lastName%22%3A%22Saint-Amand%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Brian%20K.%22%2C%22lastName%22%3A%22Walker%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Joana%22%2C%22lastName%22%3A%22Figueiredo%22%7D%5D%2C%22abstractNote%22%3A%22Since%20the%201980s%2C%20populations%20of%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20Acropora%20cervicornis%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20and%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20A.%20palmata%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20have%20experienced%20severe%20declines%20due%20to%20disease%20and%20anthropogenic%20stressors%3B%20resulting%20in%20their%20listing%20as%20threatened%2C%20and%20their%20need%20for%20restoration.%20In%20this%20study%2C%20larval%20survival%20and%20competency%20data%20were%20collected%20and%20used%20to%20calibrate%20a%20very%20high-resolution%20hydrodynamic%20model%20%28up%20to%20100m%29%20to%20determine%20the%20dispersal%20patterns%20of%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20Acropora%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20species%20along%20the%20Florida%5Cu2019s%20Coral%20Reef.%20The%20resulting%20connectivity%20matrices%20was%20incorporated%20into%20a%20metapopulation%20model%20to%20compare%20strategies%20for%20restoring%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20Acropora%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20populations.%20This%20study%20found%20that%20Florida%5Cu2019s%20Coral%20Reef%20was%20historically%20a%20well-connected%20system%2C%20and%20that%20spatially%20selective%20restoration%20may%20be%20able%20to%20stimulate%20natural%20recovery.%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20Acropora%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20larvae%20are%20predominantly%20transported%20northward%20along%20the%20Florida%5Cu2019s%20Coral%20Reef%2C%20however%20southward%20transport%20also%20occurs%2C%20driven%20by%20tides%20and%20baroclinic%20eddies.%20Local%20retention%20and%20self-recruitment%20processes%20were%20strong%20for%20a%20broadcast%20spawner%20with%20a%20long%20pelagic%20larval%20duration.%20Model%20simulations%20demonstrate%20that%20it%20is%20beneficial%20to%20spread%20restoration%20effort%20across%20more%20reefs%2C%20rather%20than%20focusing%20on%20a%20few%20reefs.%20Differences%20in%20population%20patchiness%20between%20the%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20Acropora%20cervicornis%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20and%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20A.%20palmata%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20drive%20the%20need%20for%20different%20approaches%20to%20their%20management%20plans.%20This%20model%20can%20be%20used%20as%20a%20tool%20to%20address%20the%20species-specific%20management%20to%20restore%20genotypically%20diverse%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20Acropora%5Cn%20%20%20%20%20%20%20%20%20%20%20%20%20%20populations%20on%20the%20Florida%5Cu2019s%20Coral%20Reef%2C%20and%20its%20methods%20could%20be%20expanded%20to%20other%20vulnerable%20populations.%22%2C%22date%22%3A%222023-1-17%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.3389%5C%2Ffmars.2022.1038463%22%2C%22ISSN%22%3A%222296-7745%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.frontiersin.org%5C%2Farticles%5C%2F10.3389%5C%2Ffmars.2022.1038463%5C%2Ffull%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-01-24T09%3A34%3A07Z%22%7D%7D%2C%7B%22key%22%3A%22M6RKKS6A%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Sampurno%20et%20al.%22%2C%22parsedDate%22%3A%222023-01-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BSampurno%2C%20J.%2C%20Ardianto%2C%20R.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282023%29.%20Integrated%20machine%20learning%20and%20GIS-based%20bathtub%20models%20to%20assess%20the%20future%20flood%20risk%20in%20the%20Kapuas%20River%20Delta%2C%20Indonesia.%20%26lt%3Bi%26gt%3BJournal%20of%20Hydroinformatics%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B25%26lt%3B%5C%2Fi%26gt%3B%281%29%2C%20113%26%23x2013%3B125.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.2166%5C%2Fhydro.2022.106%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.2166%5C%2Fhydro.2022.106%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Integrated%20machine%20learning%20and%20GIS-based%20bathtub%20models%20to%20assess%20the%20future%20flood%20risk%20in%20the%20Kapuas%20River%20Delta%2C%20Indonesia%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Joko%22%2C%22lastName%22%3A%22Sampurno%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Randy%22%2C%22lastName%22%3A%22Ardianto%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22As%20more%20and%20more%20people%20live%20near%20the%20sea%2C%20future%20%5Cufb02ood%20risk%20must%20be%20properly%20assessed%20for%20sustainable%20urban%20planning%20and%20coastal%20protection.%20However%2C%20this%20is%20rarely%20the%20case%20in%20developing%20countries%20where%20there%20is%20a%20lack%20of%20both%20in-situ%20data%20collection%20and%20forecasting%20tools.%20Here%2C%20we%20consider%20the%20case%20of%20the%20Kapuas%20River%20Delta%20%28KRD%29%2C%20a%20data-scarce%20delta%20on%20the%20west%20coast%20of%20Borneo%20Island%2C%20Indonesia.%20We%20assessed%20future%20%5Cufb02ood%20risk%20under%20three%20climate%20change%20scenarios%20%28RCP2.6%2C%20RCP4.5%2C%20and%20RCP8.5%29.%20We%20combined%20the%20multiple%20linear%20regression%20and%20the%20GIS-based%20bathtub%20inundation%20models%20to%20assess%20the%20future%20%5Cufb02ood%20risk.%20The%20former%20model%20was%20implemented%20to%20model%20the%20river%5Cu2019s%20water-level%20dynamics%20in%20the%20KRD%2C%20particularly%20in%20Pontianak%2C%20under%20the%20in%5Cufb02uence%20of%20rainfall%20changes%2C%20surface%20wind%20changes%2C%20and%20sea-level%20rise.%20The%20later%20model%20created%20%5Cufb02ood%20maps%20with%20inundated%20areas%20under%20a%20100-year%20%5Cufb02ood%20scenario%2C%20representing%20Pontianak%5Cu2019s%20current%20and%20future%20%5Cufb02ood%20extent.%20We%20found%20that%20about%206.4%25%5Cu201311.9%25%20more%20buildings%20and%20about%206.8%25%5Cu201312.7%25%20more%20roads%20will%20be%20impacted%20by%20a%20100-year%20%5Cufb02ood%20in%202100.%20Our%20assessment%20guides%20the%20local%20water%20manager%20in%20preparing%20adequate%20%5Cufb02ood%20mitigation%20strategies.%22%2C%22date%22%3A%222023-01-01%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.2166%5C%2Fhydro.2022.106%22%2C%22ISSN%22%3A%221464-7141%2C%201465-1734%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fiwaponline.com%5C%2Fjh%5C%2Farticle%5C%2F25%5C%2F1%5C%2F113%5C%2F92197%5C%2FIntegrated-machine-learning-and-GIS-based-bathtub%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-02-02T08%3A09%3A41Z%22%7D%7D%2C%7B%22key%22%3A%22KJRUBWX9%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Saint-Amand%20et%20al.%22%2C%22parsedDate%22%3A%222023%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BSaint-Amand%2C%20A.%2C%20Lambrechts%2C%20J.%2C%20Thomas%2C%20C.%20J.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282023%29.%20How%20fine%20is%20fine%20enough%3F%20Effect%20of%20mesh%20resolution%20on%20hydrodynamic%20simulations%20in%20coral%20reef%20environments.%20%26lt%3Bi%26gt%3BOcean%20Modelling%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B186%26lt%3B%5C%2Fi%26gt%3B%2C%20102254.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2023.102254%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2023.102254%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22How%20fine%20is%20fine%20enough%3F%20Effect%20of%20mesh%20resolution%20on%20hydrodynamic%20simulations%20in%20coral%20reef%20environments%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Antoine%22%2C%22lastName%22%3A%22Saint-Amand%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Christopher%20J.%22%2C%22lastName%22%3A%22Thomas%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22Coral%20reef%20environments%20are%20biodiversity%20hotspots%20that%20provide%20many%20services%20to%20coastal%20communities.%20They%20are%20currently%20facing%20an%20increasing%20anthropogenic%20pressure%20that%20jeopardises%20their%20survival.%20Numerical%20ocean%20models%20are%20an%20important%20tool%20to%20understand%20the%20functioning%20of%20coral%20ecosystems%20and%20the%20mechanisms%20ensuring%20their%20resilience.%20However%2C%20simulating%20the%20water%20circulation%20through%20reef%20systems%20is%20challenging%20because%20of%20their%20naturally%20complex%20topography%20and%20bathymetry.%20Many%20ocean%20models%20used%20for%20such%20applications%20have%20a%20spatial%20resolution%20coarser%20than%20the%20scale%20of%20individual%20reefs%2C%20which%20puts%20into%20question%20their%20suitability%20for%20the%20task.%20Here%2C%20we%20assess%20the%20sensitivity%20of%20a%20coastal%20ocean%20model%5Cu2019s%20outputs%20to%20its%20spatial%20resolution%20when%20simulating%20the%20water%20circulation%20in%20the%20entire%20Great%20Barrier%20Reef%20%28Australia%29%2C%20the%20largest%20coral%20reef%20system%20in%20the%20world.%20We%20consider%20the%20same%20model%20with%20five%20different%20resolutions%20near%20reefs%2C%20ranging%20from%20250%20m%20to%204%20km%2C%20and%20compare%20the%20model%20outputs%20at%20different%20locations%20around%20reefs%20and%20in%20the%20open%20ocean.%20We%20also%20simulate%20the%20transport%20of%20passive%20particles%20released%20from%20those%20different%20locations.%20Our%20results%20show%20that%20the%20simulated%20tidal%20signal%20is%20similar%20for%20all%20five%20resolutions.%20However%2C%20strong%20discrepancies%20%28%26gt%3B%2010%20cm%5C%2Fs%29%20in%20the%20current%20velocity%20are%20observed%20near%20the%20reefs%20and%20along%20the%20rugged%20coastline.%20When%20using%20a%20coarse-resolution%20model%2C%20the%20amplitude%20of%20the%20currents%20is%20overestimated%20over%20reefs%2C%20and%20underestimated%20between%20them.%20We%20find%20that%20validating%20the%20model%20at%20deep%20water%20mooring%20sites%20is%20not%20sufficient%20to%20ensure%20it%20performs%20well%20close%20to%20reefs.%20Discrepancies%20in%20currents%20lead%20to%20more%20directional%20and%20uniform%20tracer%20dispersal%20patterns%20on%20coarse-resolution%20meshes%20that%20contrast%20with%20the%20more%20dispersive%20patterns%20observed%20on%20fine-resolution%20meshes.%20Those%20differences%20at%20the%20reef%20level%20have%20a%20large%20cumulative%20effect%20when%20simulating%20transport%20processes%20over%20several%20weeks.%20Our%20results%20suggest%20that%20ocean%20circulation%20and%20transport%20simulations%20in%20coral%20reef%20environments%20should%20be%20based%20on%20model%20resolutions%20finer%20than%20the%20reef%20scale%2C%20which%20generally%20means%20a%20maximum%20resolution%20of%20about%20250%5Cu2013500%20m.%22%2C%22date%22%3A%2212%5C%2F2023%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ocemod.2023.102254%22%2C%22ISSN%22%3A%2214635003%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS1463500323000951%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-09-07T11%3A09%3A50Z%22%7D%7D%2C%7B%22key%22%3A%22WZ6S8MTN%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Verhofstede%20et%20al.%22%2C%22parsedDate%22%3A%222023%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BVerhofstede%2C%20A.%2C%20Dobbelaere%2C%20T.%2C%20Harlay%2C%20J.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282023%29.%20Seychelles%20Plateau%26%23x2019%3Bs%20oil%20spill%20vulnerability.%20%26lt%3Bi%26gt%3BMarine%20Pollution%20Bulletin%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B196%26lt%3B%5C%2Fi%26gt%3B%2C%20115652.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.marpolbul.2023.115652%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.marpolbul.2023.115652%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Seychelles%20Plateau%27s%20oil%20spill%20vulnerability%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Alex%22%2C%22lastName%22%3A%22Verhofstede%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Dobbelaere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22J%5Cu00e9r%5Cu00f4me%22%2C%22lastName%22%3A%22Harlay%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22Small%20Island%20Developing%20States%2C%20such%20as%20Seychelles%2C%20are%20highly%20susceptible%20to%20oil%20pollution%20incidents%2C%20with%20limited%20infrastructure%20for%20detection%20and%20mitigation.%20While%20an%20oil%20spill%20could%20significantly%20impact%20Seychelle%5Cu2019s%20tourism%20industry%2C%20contributing%20to%20~40%25%20of%20its%20GDP%2C%20the%20archipelago%5Cu2019s%20vulnerability%20remains%20largely%20unknown.%20Here%2C%20we%20developed%20a%20high-resolution%20ocean%20circulation%20model%20for%20Seychelles%20Plateau%2C%20simulating%20currents%20over%20three%20years%20%282018%5Cu20132020%29%20to%20model%20oil%20spill%20dispersal%20to%20six%20ecologically%20and%20economically%20significant%20coastal%20areas.%20Our%20findings%20reveal%20distinct%20seasonality%20in%20offshore%20risk%20distribution%2C%20driven%20by%20seasonal%20fluctuations%20in%20atmospheric%20and%20oceanic%20circulations.%20We%20show%20that%20an%20oil%20spill%20originating%20from%20any%20part%20of%20the%20plateau%20could%20potentially%20impact%20a%20sensitive%20coastal%20site%20in%20less%20than%20five%20days.%20By%20identifying%20high-risk%20areas%2C%20including%20the%20major%20northsouth%20shipping%20route%2C%20we%20emphasize%20the%20importance%20of%20close%20satellite%20and%20airborne%20monitoring%20for%20early%20warn%5Cu00ad%20ings%20to%20protect%20Seychelles%5Cu2019%20coastal%20ecosystems%20and%20tourism%20industry.%22%2C%22date%22%3A%2211%5C%2F2023%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.marpolbul.2023.115652%22%2C%22ISSN%22%3A%220025326X%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0025326X23010871%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-10-19T06%3A35%3A39Z%22%7D%7D%2C%7B%22key%22%3A%22LGUNY9L7%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Patterson%20et%20al.%22%2C%22parsedDate%22%3A%222023%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BPatterson%2C%20R.%20G.%2C%20Wolanski%2C%20E.%2C%20Groom%2C%20R.%2C%20Critchell%2C%20K.%2C%20Playford%2C%20L.%2C%20Grubert%2C%20M.%2C%20Kennett%2C%20R.%2C%20Tait%2C%20H.%2C%20Udyawer%2C%20V.%2C%20Lambrechts%2C%20J.%2C%20%26amp%3B%20Campbell%2C%20H.%20A.%20%282023%29.%20Improving%20certainty%20in%20marine%20ecosystems%3A%20A%20biophysical%20modelling%20approach%20in%20the%20remote%2C%20data-limited%20Gulf%20of%20Carpentaria.%20%26lt%3Bi%26gt%3BEstuarine%2C%20Coastal%20and%20Shelf%20Science%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B283%26lt%3B%5C%2Fi%26gt%3B%2C%20108254.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecss.2023.108254%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecss.2023.108254%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Improving%20certainty%20in%20marine%20ecosystems%3A%20A%20biophysical%20modelling%20approach%20in%20the%20remote%2C%20data-limited%20Gulf%20of%20Carpentaria%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ruth%20G.%22%2C%22lastName%22%3A%22Patterson%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Wolanski%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Rachel%22%2C%22lastName%22%3A%22Groom%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Kay%22%2C%22lastName%22%3A%22Critchell%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Luke%22%2C%22lastName%22%3A%22Playford%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Mark%22%2C%22lastName%22%3A%22Grubert%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Rod%22%2C%22lastName%22%3A%22Kennett%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Heidi%22%2C%22lastName%22%3A%22Tait%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vinay%22%2C%22lastName%22%3A%22Udyawer%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Hamish%20A.%22%2C%22lastName%22%3A%22Campbell%22%7D%5D%2C%22abstractNote%22%3A%22Remote%2C%20data-limited%20marine%20environments%20are%20poorly%20understood%2C%20making%20conservation%20and%20resource%20manage%5Cu00ad%20ment%20major%20challenges%20in%20the%20rapidly%20changing%20environment.%20High%20field%20data%20collection%20costs%20results%20in%20sparse%20data%2C%20which%20limits%20the%20traditional%20scientific%20approach%20to%20understand%20the%20functioning%20of%20these%20remote%20ecosystems.%20The%20Gulf%20of%20Carpentaria%20is%20a%20vast%2C%20remote%20and%20data-limited%20region%20in%20northern%20Australia%20that%20is%20vulnerable%20to%20rapid%20changes%20due%20to%20climate%20change%20and%20externally%20derived%20marine%20debris%2C%20but%20extremely%20difficult%20and%20costly%20to%20access.%20This%20study%20aimed%20to%20test%20a%20method%20of%20improving%20certainty%20in%20ecological%20and%20physical%20processes%20in%20the%20Gulf%20of%20Carpentaria%20by%20maximising%20the%20use%20of%20alternative%20biophysical%20data%20from%20local%20Indigenous-owned%20and%20managed%20land%20and%20sea%20country%2C%20to%20elucidate%20the%20ecosystem%20functioning.%20We%20investigated%20the%20role%20of%20currents%20and%20wind%20in%20previously%20published%20Green%20turtle%20%28Chelonia%20mydas%29%20post-nesting%20satellite%20tracking%20migration%20data%2C%20and%20found%20they%20had%20no%20influence%20on%20the%20turtles%5Cu2019%20migration%20path.%20We%20also%20found%20that%20turtles%20did%20not%20use%20compass%20bearing%20alone%20to%20make%20their%20migration%2C%20rather%20they%20seemingly%20used%20coastal%20cues%20to%20%5Cu2019leap-frog%5Cu2019%20along%20the%20coastline%20until%20they%20reached%20their%20foraging%20grounds.%20Next%2C%20we%20identified%20the%20spatio-temporal%20distribution%20of%20floating%20marine%20plastics%20using%20Indigenous-lead%20citizen%20science%20coastal%20marine%20debris%20surveys%2C%20and%20found%20that%20previous%20studies%20have%20underestimated%20marine%20debris%20presence%20in%20the%20region.%20Finally%2C%20biophysical%20modelling%20suggests%20that%20large%20migra%5Cu00ad%20tions%20%28%26gt%3B200%20km%20in%2028%5Cu201335%20days%29%20of%20tagged%20male%20Giant%20mud%20crabs%20%28Scylla%20serrata%29%20against%20prevailing%20winds%2C%20currents%20and%20tides%20were%20possible%20by%20using%20selective%20tidal%20stream%20transport%20and%20directional%20swimming.%20These%20case-studies%20demonstrate%20the%20effectiveness%20of%20explorative%20biophysical%20modelling%20supported%20by%20alternative%20field%20data%2C%20and%20improve%20certainty%20in%20ecological%20processes%20with%20significance%20in%20culture%2C%20conservation%20and%20commercial%20values%20in%20the%20region.%22%2C%22date%22%3A%2204%5C%2F2023%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ecss.2023.108254%22%2C%22ISSN%22%3A%2202727714%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0272771423000446%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-03-05T15%3A26%3A17Z%22%7D%7D%2C%7B%22key%22%3A%224VPNU53Z%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Hanert%20et%20al.%22%2C%22parsedDate%22%3A%222023%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BHanert%2C%20E.%2C%20Mohammed%2C%20A.%20V.%2C%20Veerasingam%2C%20S.%2C%20Dobbelaere%2C%20T.%2C%20Vallaeys%2C%20V.%2C%20%26amp%3B%20Vethamony%2C%20P.%20%282023%29.%20A%20multiscale%20ocean%20modelling%20system%20for%20the%20central%20Arabian%5C%2FPersian%20Gulf%3A%20From%20regional%20to%20structure%20scale%20circulation%20patterns.%20%26lt%3Bi%26gt%3BEstuarine%2C%20Coastal%20and%20Shelf%20Science%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B282%26lt%3B%5C%2Fi%26gt%3B%2C%20108230.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecss.2023.108230%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecss.2023.108230%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20multiscale%20ocean%20modelling%20system%20for%20the%20central%20Arabian%5C%2FPersian%20Gulf%3A%20From%20regional%20to%20structure%20scale%20circulation%20patterns%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Aboobacker%20Valliyil%22%2C%22lastName%22%3A%22Mohammed%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Subramanian%22%2C%22lastName%22%3A%22Veerasingam%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Dobbelaere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Valentin%22%2C%22lastName%22%3A%22Vallaeys%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ponnumony%22%2C%22lastName%22%3A%22Vethamony%22%7D%5D%2C%22abstractNote%22%3A%22The%20Arabian%5C%2FPersian%20Gulf%20%28hereafter%2C%20the%20%5Cu2018%5Cu2018Gulf%5Cu2019%5Cu2019%29%20is%20one%20the%20busiest%20and%20fastest%20changing%20sea%20in%20the%20World.%20Its%20circulation%20is%20primarily%20driven%20by%20the%20surface%20water%20inflow%20from%20the%20Sea%20of%20Oman%20and%20density-driven%20and%20wind-driven%20flows%20within%20the%20Gulf.%20The%20regional%20circulation%20in%20its%20central%20part%2C%20particularly%20around%20Qatar%2C%20could%20not%20be%20explored%20because%20of%20unavailability%20of%20measured%20current%20data%20and%20the%20coarse%20resolution%20opted%20for%20the%20entire%20Gulf%20modelling.%20In%20the%20present%20study%2C%20we%20developed%20a%20high-resolution%20ocean%20modelling%20system%20of%20the%20entire%20Gulf%20with%20a%20particular%20focus%20on%20Qatar%20coastal%20waters.%20The%20model%20uses%20an%20unstructured%20mesh%20with%20different%20resolutions%20ranging%20from%20%5Cu223c5%20km%20in%20the%20open%20ocean%20to%20%5Cu223c150%20m%20along%20the%20coast%20of%20Qatar%20and%20less%20than%2040%20m%20around%20artificial%20structures.%20The%20model%20results%20have%20been%20validated%20with%20in%20situ%20data%20collected%20off%20Qatar.%20It%20allows%20seamless%20simulations%20of%20hydrodynamic%20processes%20from%20the%20entire%20basin%20scale%20down%20to%20the%20scale%20of%20coastal%20structures.%20The%20study%20identifies%20seasonal%20variability%20in%20currents%20and%20eddies%20in%20the%20central%20part%20of%20the%20Gulf.%20It%20also%20suggests%20the%20existence%20of%20four%20prominent%20anticyclonic%20eddies%20in%20the%20Gulf%20of%20Salwa%2C%20south%20of%20Bahrain.%20At%20the%20structure%20scale%2C%20the%20flow%20is%20mostly%20tidally%20driven%20and%20can%20be%20intensified%20beyond%201%20m%5C%2Fs%20through%20narrow%20passages%20such%20as%20between%20breakwaters%20or%20within%20artificial%20waterways.%20By%20explicitly%20representing%20the%20effect%20of%20ocean%20sprawl%20on%20the%20coastal%20circulation%2C%20our%20model%20has%20the%20potential%20to%20greatly%20improve%20the%20environmental%20impact%20assessment%20of%20coastal%20developments%20in%20the%20Gulf%20area.%22%2C%22date%22%3A%2203%5C%2F2023%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ecss.2023.108230%22%2C%22ISSN%22%3A%2202727714%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0272771423000203%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-01-23T19%3A55%3A19Z%22%7D%7D%2C%7B%22key%22%3A%22ZLWJG9LY%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Sampurno%20et%20al.%22%2C%22parsedDate%22%3A%222022-08-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BSampurno%2C%20J.%2C%20Vallaeys%2C%20V.%2C%20Ardianto%2C%20R.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282022%29.%20Integrated%20hydrodynamic%20and%20machine%20learning%20models%20for%20compound%20flooding%20prediction%20in%20a%20data-scarce%20estuarine%20delta.%20%26lt%3Bi%26gt%3BNonlinear%20Processes%20in%20Geophysics%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B29%26lt%3B%5C%2Fi%26gt%3B%283%29%2C%20301%26%23x2013%3B315.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.5194%5C%2Fnpg-29-301-2022%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.5194%5C%2Fnpg-29-301-2022%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Integrated%20hydrodynamic%20and%20machine%20learning%20models%20for%20compound%20flooding%20prediction%20in%20a%20data-scarce%20estuarine%20delta%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Joko%22%2C%22lastName%22%3A%22Sampurno%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Valentin%22%2C%22lastName%22%3A%22Vallaeys%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Randy%22%2C%22lastName%22%3A%22Ardianto%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22Flood%20forecasting%20based%20on%20hydrodynamic%20modeling%20is%20an%20essential%20non-structural%20measure%20against%20compound%20%5Cufb02ooding%20across%20the%20globe.%20With%20the%20risk%20increasing%20under%20climate%20change%2C%20all%20coastal%20areas%20are%20now%20in%20need%20of%20%5Cufb02ood%20risk%20management%20strategies.%20Unfortunately%2C%20for%20local%20water%20management%20agencies%20in%20developing%20countries%2C%20building%20such%20a%20model%20is%20challenging%20due%20to%20the%20limited%20computational%20resources%20and%20the%20scarcity%20of%20observational%20data.%20We%20attempt%20to%20solve%20this%20issue%20by%20proposing%20an%20integrated%20hydrodynamic%20and%20machine%20learning%20%28ML%29%20approach%20to%20predict%20water%20level%20dynamics%20as%20a%20proxy%20for%20the%20risk%20of%20compound%20%5Cufb02ooding%20in%20a%20data-scarce%20delta.%20As%20a%20case%20study%2C%20this%20integrated%20approach%20is%20implemented%20in%20Pontianak%2C%20the%20densest%20coastal%20urban%20area%20over%20the%20Kapuas%20River%20delta%2C%20Indonesia.%20Firstly%2C%20we%20build%20a%20hydrodynamic%20model%20to%20simulate%20several%20compound%20%5Cufb02ooding%20scenarios.%20The%20outputs%20are%20then%20used%20to%20train%20the%20ML%20model.%20To%20obtain%20a%20robust%20ML%20model%2C%20we%20consider%20three%20ML%20algorithms%2C%20i.e.%2C%20random%20forest%20%28RF%29%2C%20multiple%20linear%20regression%20%28MLR%29%2C%20and%20support%20vector%20machine%20%28SVM%29.%20Our%20results%20show%20that%20the%20integrated%20scheme%20works%20well.%20The%20RF%20is%20the%20most%20accurate%20algorithm%20to%20model%20water%20level%20dynamics%20in%20the%20study%20area.%20Meanwhile%2C%20the%20ML%20model%20using%20the%20RF%20algorithm%20can%20predict%2011%20out%20of%2017%20compound%20%5Cufb02ooding%20events%20during%20the%20implementation%20phase.%20It%20could%20be%20concluded%20that%20RF%20is%20the%20most%20appropriate%20algorithm%20to%20build%20a%20reliable%20ML%20model%20capable%20of%20estimating%20the%20river%5Cu2019s%20water%20level%20dynamics%20within%20Pontianak%2C%20whose%20output%20can%20be%20used%20as%20a%20proxy%20for%20predicting%20compound%20%5Cufb02ooding%20events%20in%20the%20city.%22%2C%22date%22%3A%222022-08-01%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.5194%5C%2Fnpg-29-301-2022%22%2C%22ISSN%22%3A%221607-7946%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fnpg.copernicus.org%5C%2Farticles%5C%2F29%5C%2F301%5C%2F2022%5C%2F%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222022-08-04T07%3A27%3A11Z%22%7D%7D%2C%7B%22key%22%3A%2238RMCSFJ%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Sampurno%20et%20al.%22%2C%22parsedDate%22%3A%222022-06-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BSampurno%2C%20J.%2C%20Vallaeys%2C%20V.%2C%20Ardianto%2C%20R.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282022%29.%20Modeling%20interactions%20between%20tides%2C%20storm%20surges%2C%20and%20river%20discharges%20in%20the%20Kapuas%20River%20delta.%20%26lt%3Bi%26gt%3BBiogeosciences%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B19%26lt%3B%5C%2Fi%26gt%3B%2810%29%2C%202741%26%23x2013%3B2757.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.5194%5C%2Fbg-19-2741-2022%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.5194%5C%2Fbg-19-2741-2022%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Modeling%20interactions%20between%20tides%2C%20storm%20surges%2C%20and%20river%20discharges%20in%20the%20Kapuas%20River%20delta%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Joko%22%2C%22lastName%22%3A%22Sampurno%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Valentin%22%2C%22lastName%22%3A%22Vallaeys%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Randy%22%2C%22lastName%22%3A%22Ardianto%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22Abstract.%20The%20Kapuas%20River%20delta%20is%20a%20unique%20estuary%20system%20on%20the%20western%20coast%20of%20the%20island%20of%20Borneo%2C%20Indonesia.%20Its%20hydrodynamics%20are%20driven%20by%20an%20interplay%5Cnbetween%20storm%20surges%2C%20tides%2C%20and%20river%20discharges.%20These%20interactions%20are%20likely%20to%20be%20exacerbated%20by%20global%20warming%2C%20leading%20to%20more%20frequent%5Cncompound%20flooding%20in%20the%20area.%20The%20mechanisms%20driving%20compound%20flooding%20events%20in%20the%20Kapuas%20River%20delta%20remain%2C%20however%2C%20poorly%20known.%20Here%20we%5Cnattempt%20to%20fill%20this%20gap%20by%20assessing%20the%20interactions%20between%20river%20discharges%2C%20tides%2C%20and%20storm%20surges%20and%20how%20they%20can%20drive%20a%20compound%5Cninundation%20over%20the%20riverbanks%2C%20particularly%20within%20Pontianak%2C%20the%20main%20city%20along%20the%20Kapuas%20River.%20We%20simulated%20these%20interactions%20using%20the%5Cnmulti-scale%20hydrodynamic%20model%20SLIM%20%28Second-generation%20Louvain-la-Neuve%20Ice-ocean%20Model%29.%20Our%20model%20correctly%20reproduces%20the%20Kapuas%20River%26%23039%3Bs%20hydrodynamics%20and%20its%20interactions%20with%20tides%20and%20storm%20surge%5Cnfrom%20the%20Karimata%20Strait.%20We%20considered%20several%20extreme-scenario%20test%20cases%20to%20evaluate%20the%20impact%20of%20tide%5Cu2013storm%5Cu2013discharge%20interactions%20on%20the%5Cnmaximum%20water%20level%20profile%20from%20the%20river%20mouth%20to%20the%20upstream%20part%20of%20the%20river.%20Based%20on%20the%20maximum%20water%20level%20profiles%2C%20we%20divide%20the%20Kapuas%5CnRiver%26%23039%3Bs%20stream%20into%20three%20zones%2C%20i.e.%2C%20the%20tidally%20dominated%20region%20%28from%20the%20river%20mouth%20to%20about%2030%5Cu2009km%20upstream%29%2C%20the%20transition%20region%5Cn%28from%20about%2030%5Cu2009km%20to%20about%20150%5Cu2009km%20upstream%29%2C%20and%20the%20river-dominated%20region%20%28beyond%20150%5Cu2009km%20upstream%29.%20Thus%2C%20the%20local%20water%5Cnmanagement%20can%20define%20proper%20mitigation%20for%20handling%20compound%20flooding%20hazards%20along%20the%20riverbanks%20by%20using%20this%20zoning%20category.%20The%20model%20also%5Cnsuccessfully%20reproduced%20a%20compound%20flooding%20event%20in%20Pontianak%2C%20which%20occurred%20on%2029%5Cu00a0December%202018.%20For%20this%20event%2C%20the%20wind-generated%20surge%5Cnappeared%20to%20be%20the%20dominant%20trigger.%22%2C%22date%22%3A%222022-06-01%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.5194%5C%2Fbg-19-2741-2022%22%2C%22ISSN%22%3A%221726-4189%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fbg.copernicus.org%5C%2Farticles%5C%2F19%5C%2F2741%5C%2F2022%5C%2F%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222022-07-11T07%3A14%3A55Z%22%7D%7D%2C%7B%22key%22%3A%22BHDR9X5N%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Sampurno%20et%20al.%22%2C%22parsedDate%22%3A%222022-06-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BSampurno%2C%20J.%2C%20Vallaeys%2C%20V.%2C%20Ardianto%2C%20R.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282022%29.%20Modeling%20interactions%20between%20tides%2C%20storm%20surges%2C%20and%20river%20discharges%20in%20the%20Kapuas%20River%20delta.%20%26lt%3Bi%26gt%3BBiogeosciences%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B19%26lt%3B%5C%2Fi%26gt%3B%2810%29%2C%202741%26%23x2013%3B2757.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.5194%5C%2Fbg-19-2741-2022%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.5194%5C%2Fbg-19-2741-2022%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Modeling%20interactions%20between%20tides%2C%20storm%20surges%2C%20and%20river%20discharges%20in%20the%20Kapuas%20River%20delta%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Joko%22%2C%22lastName%22%3A%22Sampurno%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Valentin%22%2C%22lastName%22%3A%22Vallaeys%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Randy%22%2C%22lastName%22%3A%22Ardianto%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22Abstract.%20The%20Kapuas%20River%20delta%20is%20a%20unique%20estuary%20system%20on%20the%20western%20coast%20of%20the%20island%20of%20Borneo%2C%20Indonesia.%20Its%20hydrodynamics%20are%20driven%20by%20an%20interplay%5Cnbetween%20storm%20surges%2C%20tides%2C%20and%20river%20discharges.%20These%20interactions%20are%20likely%20to%20be%20exacerbated%20by%20global%20warming%2C%20leading%20to%20more%20frequent%5Cncompound%20flooding%20in%20the%20area.%20The%20mechanisms%20driving%20compound%20flooding%20events%20in%20the%20Kapuas%20River%20delta%20remain%2C%20however%2C%20poorly%20known.%20Here%20we%5Cnattempt%20to%20fill%20this%20gap%20by%20assessing%20the%20interactions%20between%20river%20discharges%2C%20tides%2C%20and%20storm%20surges%20and%20how%20they%20can%20drive%20a%20compound%5Cninundation%20over%20the%20riverbanks%2C%20particularly%20within%20Pontianak%2C%20the%20main%20city%20along%20the%20Kapuas%20River.%20We%20simulated%20these%20interactions%20using%20the%5Cnmulti-scale%20hydrodynamic%20model%20SLIM%20%28Second-generation%20Louvain-la-Neuve%20Ice-ocean%20Model%29.%20Our%20model%20correctly%20reproduces%20the%20Kapuas%20River%26%23039%3Bs%20hydrodynamics%20and%20its%20interactions%20with%20tides%20and%20storm%20surge%5Cnfrom%20the%20Karimata%20Strait.%20We%20considered%20several%20extreme-scenario%20test%20cases%20to%20evaluate%20the%20impact%20of%20tide%5Cu2013storm%5Cu2013discharge%20interactions%20on%20the%5Cnmaximum%20water%20level%20profile%20from%20the%20river%20mouth%20to%20the%20upstream%20part%20of%20the%20river.%20Based%20on%20the%20maximum%20water%20level%20profiles%2C%20we%20divide%20the%20Kapuas%5CnRiver%26%23039%3Bs%20stream%20into%20three%20zones%2C%20i.e.%2C%20the%20tidally%20dominated%20region%20%28from%20the%20river%20mouth%20to%20about%2030%5Cu2009km%20upstream%29%2C%20the%20transition%20region%5Cn%28from%20about%2030%5Cu2009km%20to%20about%20150%5Cu2009km%20upstream%29%2C%20and%20the%20river-dominated%20region%20%28beyond%20150%5Cu2009km%20upstream%29.%20Thus%2C%20the%20local%20water%5Cnmanagement%20can%20define%20proper%20mitigation%20for%20handling%20compound%20flooding%20hazards%20along%20the%20riverbanks%20by%20using%20this%20zoning%20category.%20The%20model%20also%5Cnsuccessfully%20reproduced%20a%20compound%20flooding%20event%20in%20Pontianak%2C%20which%20occurred%20on%2029%5Cu00a0December%202018.%20For%20this%20event%2C%20the%20wind-generated%20surge%5Cnappeared%20to%20be%20the%20dominant%20trigger.%22%2C%22date%22%3A%222022-06-01%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.5194%5C%2Fbg-19-2741-2022%22%2C%22ISSN%22%3A%221726-4189%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fbg.copernicus.org%5C%2Farticles%5C%2F19%5C%2F2741%5C%2F2022%5C%2F%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222022-06-01T09%3A01%3A54Z%22%7D%7D%2C%7B%22key%22%3A%22IZBNJ472%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Saint-Amand%20et%20al.%22%2C%22parsedDate%22%3A%222022-04-22%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BSaint-Amand%2C%20A.%2C%20Grech%2C%20A.%2C%20Choukroun%2C%20S.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282022%29.%20Quantifying%20the%20environmental%20impact%20of%20a%20major%20coal%20mine%20project%20on%20the%20adjacent%20Great%20Barrier%20Reef%20ecosystems.%20%26lt%3Bi%26gt%3BMarine%20Pollution%20Bulletin%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B179%26lt%3B%5C%2Fi%26gt%3B%2C%20113556.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2Fj.marpolbul.2022.113656%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2Fj.marpolbul.2022.113656%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Quantifying%20the%20environmental%20impact%20of%20a%20major%20coal%20mine%20project%20on%20the%20adjacent%20Great%20Barrier%20Reef%20ecosystems%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Antoine%22%2C%22lastName%22%3A%22Saint-Amand%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Alana%22%2C%22lastName%22%3A%22Grech%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Severine%22%2C%22lastName%22%3A%22Choukroun%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22A%20major%20coal%20mine%20project%20in%20Queensland%2C%20Australia%2C%20is%20currently%20under%20review.%20It%20is%20planned%20to%20be%20located%20about%2010%20km%20away%20from%20the%20Great%20Barrier%20Reef%20World%20Heritage%20Area%20%28GBRWHA%29.%20Sediment%20dispersal%20patterns%20and%20their%20impact%20on%20marine%20ecosystems%20have%20not%20been%20properly%20assessed%20yet.%20Here%2C%20we%20simulate%20the%20dispersal%20of%20different%20sediment%20types%20with%20a%20high-resolution%20ocean%20model%2C%20and%20derive%20their%20environmental%20footprint.%20We%20show%20that%20sediments%20finer%20than%2032%20%5Cu03bcm%20could%20reach%20dense%20seagrass%20meadows%20and%20a%20dugong%20sanctuary%20within%20a%20few%20weeks.%20The%20intense%20tidal%20circulation%20leads%20to%20non-isotropic%20and%20long-distance%20sediment%20dispersal%20patterns%20along%20the%20coast.%20Our%20results%20suggest%20that%20the%20sediments%20released%20by%20this%20project%20will%20not%20be%20quickly%20mixed%20but%20rather%20be%20concen%5Cu00ad%20trated%20where%20the%20most%20valuable%20ecosystems%20are%20located.%20If%20accepted%2C%20this%20coal%20mine%20could%20therefore%20have%20a%20farreaching%20impact%20on%20the%20GBRWHA%20and%20its%20iconic%20marine%20species.%22%2C%22date%22%3A%222022-04-22%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%22j.marpolbul.2022.113656%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.marpolbul.2022.113656%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222022-04-26T07%3A49%3A42Z%22%7D%7D%2C%7B%22key%22%3A%22XU5UTZ42%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Dobbelaere%20et%20al.%22%2C%22parsedDate%22%3A%222022-02-08%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BDobbelaere%2C%20T.%2C%20Holstein%2C%20D.%20M.%2C%20Muller%2C%20E.%20M.%2C%20Gramer%2C%20L.%20J.%2C%20McEachron%2C%20L.%2C%20Williams%2C%20S.%20D.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282022%29.%20Connecting%20the%20Dots%3A%20Transmission%20of%20Stony%20Coral%20Tissue%20Loss%20Disease%20From%20the%20Marquesas%20to%20the%20Dry%20Tortugas.%20%26lt%3Bi%26gt%3BFrontiers%20in%20Marine%20Science%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B9%26lt%3B%5C%2Fi%26gt%3B%2C%20778938.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.3389%5C%2Ffmars.2022.778938%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.3389%5C%2Ffmars.2022.778938%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Connecting%20the%20Dots%3A%20Transmission%20of%20Stony%20Coral%20Tissue%20Loss%20Disease%20From%20the%20Marquesas%20to%20the%20Dry%20Tortugas%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Dobbelaere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Daniel%20M.%22%2C%22lastName%22%3A%22Holstein%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Erinn%20M.%22%2C%22lastName%22%3A%22Muller%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Lewis%20J.%22%2C%22lastName%22%3A%22Gramer%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Lucas%22%2C%22lastName%22%3A%22McEachron%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sara%20D.%22%2C%22lastName%22%3A%22Williams%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22For%20the%20last%207%20years%2C%20Florida%5Cu2019s%20Coral%20Reef%20%28FCR%29%20has%20suffered%20from%20widespread%20and%20severe%20coral%20loss%20caused%20by%20stony%20coral%20tissue%20loss%20disease%20%28SCTLD%29.%20First%20observed%20off%20the%20coast%20of%20Miami-Dade%20county%20in%202014%2C%20the%20outbreak%20has%20since%20spread%20throughout%20the%20entirety%20of%20FCR%20and%20some%20areas%20of%20the%20Caribbean.%20However%2C%20the%20propagation%20of%20the%20disease%20through%20FCR%20seemed%20to%20slow%20down%20when%20it%20reached%20the%20western%20end%20of%20the%20Marquesas%20in%20August%202020.%20Despite%20being%20present%20about%2030%20km%20%28%5Cu223c20%20miles%29%20from%20the%20Dry%20Tortugas%20%28DRTO%29%2C%20SCTLD%20was%20not%20reported%20in%20this%20area%20before%20May%202021.%20As%20SCTLD%20transmission%20is%20likely%20to%20be%20waterborne%2C%20here%20we%20suggest%20that%20this%20apparently%20delayed%20propagation%20is%20related%20to%20eddy%20activity%20near%20the%20DRTO%20under%20the%20influence%20of%20the%20Loop%20Current%5C%2FFlorida%20Current%20system.%20To%20quantify%20the%20impact%20of%20the%20local%20ocean%20circulation%20on%20the%20spread%20of%20SCTLD%20from%20the%20Marquesas%20and%20the%20DRTO%2C%20we%20evaluated%20the%20hydrodynamic-predicted%20connectivity%20between%20these%20two%20regions%20using%20a%20high-resolution%20hydro-epidemiological%20model%20between%20May%202018%20and%20May%202021.%20Our%20results%20suggest%20that%20the%20Marquesas%20and%20the%20DRTO%20were%20not%20connected%20during%20February-October%202020%20and%20January-May%202021.%20These%20periods%20coincided%20with%20either%20the%20occurrence%20of%20Tortugas%20gyres%20and%20mean%20circulation%20with%20an%20eastward%20component%20between%20the%20Marquesas%20and%20the%20DRTO%20or%20the%20presence%20of%20southward%20currents.%20Our%20results%20suggest%20that%20disease%20agents%20probably%20reached%20the%20DRTO%20in%20November%202020%20and%20that%20they%20most%20likely%20originated%20from%20southern%20or%20northwestern%20reefs%20of%20the%20Marquesas.%20This%20study%20provides%20novel%20insight%20into%20the%20role%20played%20by%20the%20hydrodynamics%20in%20the%20spread%20of%20SCTLD%20within%20the%20western-most%20edge%20of%20FCR%2C%20and%20in%20propagating%20the%20disease%20to%20uninfected%20locations.%22%2C%22date%22%3A%222022-2-8%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.3389%5C%2Ffmars.2022.778938%22%2C%22ISSN%22%3A%222296-7745%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.frontiersin.org%5C%2Farticles%5C%2F10.3389%5C%2Ffmars.2022.778938%5C%2Ffull%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222022-02-08T17%3A05%3A50Z%22%7D%7D%2C%7B%22key%22%3A%22RHP447JS%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Vincent%20et%20al.%22%2C%22parsedDate%22%3A%222022%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BVincent%2C%20D.%2C%20Lambrechts%2C%20J.%2C%20Tyler%2C%20R.%20H.%2C%20Karatekin%2C%20%26%23xD6%3B.%2C%20Dehant%2C%20V.%2C%20%26amp%3B%20Deleersnijder%2C%20%26%23xC9%3B.%20%282022%29.%20A%20numerical%20study%20of%20the%20liquid%20motion%20in%20Titan%26%23x2019%3Bs%20subsurface%20ocean.%20%26lt%3Bi%26gt%3BIcarus%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B388%26lt%3B%5C%2Fi%26gt%3B%2C%20115219.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.icarus.2022.115219%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.icarus.2022.115219%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20numerical%20study%20of%20the%20liquid%20motion%20in%20Titan%5Cu2019s%20subsurface%20ocean%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22David%22%2C%22lastName%22%3A%22Vincent%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Robert%20H.%22%2C%22lastName%22%3A%22Tyler%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%5Cu00d6zg%5Cu00fcr%22%2C%22lastName%22%3A%22Karatekin%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22V%5Cu00e9ronique%22%2C%22lastName%22%3A%22Dehant%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%5Cu00c9ric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22An%20ocean%20filled%20with%20liquid%20water%20lies%20beneath%20the%20icy%20surface%20of%20several%20Jovian%20and%20Saturnian%20moons.%20In%20such%20an%20ocean%2C%20the%20currents%20are%20driven%20by%20various%20phenomena%20such%20as%20the%20tidal%20forcing%2C%20the%20deformation%20of%20the%20ice%20shell%20lying%20at%20its%20top%2C%20the%20temperature%20gradient%20resulting%20from%20the%20surface%20and%20bottom%20heat%20fluxes.%20.%20.%20The%20flow%20induced%20by%20the%20first%20two%20forcings%20can%20be%20modelled%20by%20means%20of%20a%202D%20depth-averaged%20model%2C%20while%20the%20third%20one%20generates%20horizontal%20and%20vertical%20density%20variations%20whose%20effects%20can%20only%20be%20captured%20by%20a%203D%20baroclinic%20model.%22%2C%22date%22%3A%2212%5C%2F2022%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.icarus.2022.115219%22%2C%22ISSN%22%3A%2200191035%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0019103522003165%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-03-07T18%3A59%3A40Z%22%7D%7D%2C%7B%22key%22%3A%22PFFJ4E5Q%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Lopez%5Cu2010Gamundi%20et%20al.%22%2C%22parsedDate%22%3A%222022%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BLopez%26%23x2010%3BGamundi%2C%20C.%2C%20Dobbelaere%2C%20T.%2C%20Hanert%2C%20E.%2C%20Harris%2C%20P.%20M.%2C%20Eberli%2C%20G.%2C%20%26amp%3B%20Purkis%2C%20S.%20J.%20%282022%29.%20Simulating%20sedimentation%20on%20the%20Great%20Bahama%20Bank%20%26%23x2013%3B%20Sources%2C%20sinks%20and%20storms.%20%26lt%3Bi%26gt%3BSedimentology%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B69%26lt%3B%5C%2Fi%26gt%3B%287%29%2C%202693%26%23x2013%3B2714.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1111%5C%2Fsed.13020%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1111%5C%2Fsed.13020%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Simulating%20sedimentation%20on%20the%20Great%20Bahama%20Bank%20%5Cu2013%20Sources%2C%20sinks%20and%20storms%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Cecilia%22%2C%22lastName%22%3A%22Lopez%5Cu2010Gamundi%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Dobbelaere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Paul%20M.%22%2C%22lastName%22%3A%22Harris%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Gregor%22%2C%22lastName%22%3A%22Eberli%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sam%20J.%22%2C%22lastName%22%3A%22Purkis%22%7D%2C%7B%22creatorType%22%3A%22editor%22%2C%22firstName%22%3A%22Tracy%22%2C%22lastName%22%3A%22Frank%22%7D%5D%2C%22abstractNote%22%3A%22This%20study%20developed%20a%20high-%5Cufb01delity%20hydrodynamic%20simulation%20of%20sediment%20production%2C%20transport%20and%20deposition%20for%20the%20Great%20Bahama%20Bank.%20This%20model%20was%20run%20with%20a%20time-step%20of%2015%20min%20for%20the%20entirety%20of%202016%2C%20forced%20by%20tides%2C%20off-platform%20circulation%20and%20wind.%20Encompassed%20in%20this%20run%20are%20364%20days%20of%20fair-weather%20conditions%20and%20two%20days%20when%20the%20passage%20of%20Category%204%20Matthew%20brought%20hurricane-force%20winds%20to%20the%20platform.%20This%20simulation%20therefore%20offers%20an%20excellent%20opportunity%20to%20contrast%20the%20sway%20of%20fair-weather%20and%20storm-weather%20conditions%20on%20sculpting%20the%20facies%20arrangement%20atop%20this%20100%20000%20km2%20shallow-water%20carbonate%20platform.%20The%20work%20suggests%20that%20fairweather%20conditions%20are%20suf%5Cufb01cient%20to%20deliver%20the%20platform%5Cu2019s%20broad-scale%20facies%20patterns.%20Even%20the%20lethargic%20currents%20of%20the%20platform%20interior%20can%20move%20mud%20%28%26lt%3B63%20%5Cu03bcm%29%20over%20200%20km%20from%20its%20source%20over%20the%20course%20of%20one%20year.%20Intense%20focusing%20of%20tidal%20currents%20between%20islands%20and%20close%20to%20the%20platform%20margin%20are%20ample%20to%20move%20coarse%20grains%20%28%26gt%3B450%20%5Cu03bcm%29%2C%20at%20least%20locally%2C%20as%20is%20necessary%20to%20produce%20the%20vast%20ooid%20fairways%20for%20which%20the%20Great%20Bahama%20Bank%20is%20famed.%20Even%20at%20the%20height%20of%20Hurricane%20Matthew%2C%20average%20current%20speeds%20in%20these%20tidally-dominated%20areas%20do%20not%20exceed%20the%20speeds%20simulated%20for%20fairweather%20conditions.%20Hence%2C%20the%20hurricane%20has%20negligible%20effect%20in%20these%20highenergy%20areas.%20The%20hurricane%20does%20not%20have%20zero%20impact%2C%20though.%20For%20up%20to%20110%20km%20either%20side%20of%20the%20storm%5Cu2019s%20track%2C%20winds%20exceeding%2026%20m%5C%2Fs%20induce%20currents%20that%20winnow%20mud%20over%20longer%20distances%20than%20delivered%20by%20fair-weather%20conditions.%20Hence%2C%20the%20storm%20has%20a%20sedimentological%20signature%20which%2C%20albeit%20minor%2C%20might%20propagate%20into%20the%20depositional%20architecture%20of%20the%20platform%20when%20scaled%20over%20many%20storms%20through%20geological%20time.%20This%20work%20informs%20on%20the%20role%20of%20uniformitarianism%20versus%20catastrophism%20on%20carbonate%20sedimentation%20and%20casts%20doubt%20on%20geological%20interpretations%20of%20coarse-grained%20storm%20deposits%20%28tempestites%29%20atop%20shallow-water%20platforms.%22%2C%22date%22%3A%2212%5C%2F2022%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1111%5C%2Fsed.13020%22%2C%22ISSN%22%3A%220037-0746%2C%201365-3091%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fonlinelibrary.wiley.com%5C%2Fdoi%5C%2F10.1111%5C%2Fsed.13020%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222022-11-23T06%3A48%3A04Z%22%7D%7D%2C%7B%22key%22%3A%22SSCR23CJ%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Dobbelaere%20et%20al.%22%2C%22parsedDate%22%3A%222022%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BDobbelaere%2C%20T.%2C%20Curcic%2C%20M.%2C%20Le%20H%26%23xE9%3Bnaff%2C%20M.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282022%29.%20Impacts%20of%20Hurricane%20Irma%20%282017%29%20on%20wave-induced%20ocean%20transport%20processes.%20%26lt%3Bi%26gt%3BOcean%20Modelling%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B171%26lt%3B%5C%2Fi%26gt%3B%2C%20101947.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2022.101947%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2022.101947%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Impacts%20of%20Hurricane%20Irma%20%282017%29%20on%20wave-induced%20ocean%20transport%20processes%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Dobbelaere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Milan%22%2C%22lastName%22%3A%22Curcic%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Matthieu%22%2C%22lastName%22%3A%22Le%20H%5Cu00e9naff%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22The%20intensity%20of%20major%20tropical%20cyclones%20has%20increased%20during%20the%20past%20decade.%20Their%20effect%20is%20particularly%20acute%20in%20coastal%20areas%20where%20they%20cause%20extensive%20damage%20leading%20to%20an%20influx%20of%20debris%2C%20sediments%20and%20waste%20to%20the%20sea.%20However%2C%20most%20operational%20coastal%20ocean%20models%20do%20not%20represent%20heavy-wind%20transport%20processes%20correctly%20if%20the%20hydrodynamics%20is%20not%20coupled%20with%20the%20wind-generated%20waves.%20This%20may%20lead%20to%20significant%20errors%20in%20ocean%20simulations%20under%20tropical%20cyclone%20conditions.%20Here%2C%20we%20investigate%20current%5Cu2013wave%20interactions%20during%20a%20major%20hurricane%20and%20assess%20their%20impact%20on%20transport%20processes.%20We%20do%20that%20by%20coupling%20the%20unstructured-mesh%20coastal%20ocean%20model%20SLIM%20with%20the%20spectral%20wave%20model%20SWAN%2C%20and%20applying%20it%20to%20the%20Florida%20Reef%20Tract%20during%20Hurricane%20Irma%20%28September%202017%29.%20We%20show%20that%20the%20coupled%20model%20successfully%20reproduces%20the%20wave%20behavior%2C%20the%20storm%20surge%20and%20the%20ocean%20currents%20during%20the%20passage%20of%20the%20hurricane.%20We%20then%20use%20the%20coupled%20and%20uncoupled%20wave%5Cu2013current%20model%20to%20simulate%20the%20transport%20of%20passive%20drifters.%20We%20show%20that%20the%20wave%20radiation%20stress%20gradient%20alone%20can%20lead%20to%20changes%20of%20up%20to%201%20m%5C%2Fs%20in%20the%20modeled%20currents%2C%20which%20in%20turn%20leads%20to%20differences%20of%20up%20to%205%20km%20in%20the%20position%20of%20drifting%20material%20over%20the%20duration%20of%20the%20hurricane.%20The%20Stokes%20drift%20however%20appears%20to%20cause%20deflections%20up%20to%204%20times%20larger%20and%20hence%20dominates%20wave-induced%20transport.%20Wave%5Cu2013current%20interactions%20therefore%20strongly%20impact%20the%20transport%20of%20drifting%20material%20such%20as%20sediments%20and%20debris%20in%20the%20aftermath%20of%20a%20hurricane.%20They%20should%20thus%20be%20taken%20into%20account%20in%20order%20to%20correctly%20assess%20its%20overall%20impact.%22%2C%22date%22%3A%2203%5C%2F2022%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ocemod.2022.101947%22%2C%22ISSN%22%3A%2214635003%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS1463500322000026%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222022-02-05T09%3A15%3A15Z%22%7D%7D%2C%7B%22key%22%3A%22GJ35RBBW%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22lastModifiedByUser%22%3A%7B%22id%22%3A5103066%2C%22username%22%3A%22ehanert%22%2C%22name%22%3A%22%22%2C%22links%22%3A%7B%22alternate%22%3A%7B%22href%22%3A%22https%3A%5C%2F%5C%2Fwww.zotero.org%5C%2Fehanert%22%2C%22type%22%3A%22text%5C%2Fhtml%22%7D%7D%7D%2C%22creatorSummary%22%3A%22Wolanski%20and%20Hopper%22%2C%22parsedDate%22%3A%222022%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BWolanski%2C%20E.%2C%20%26amp%3B%20Hopper%2C%20C.%20%282022%29.%20Dams%20and%20climate%20change%20accelerate%20channel%20avulsion%20and%20coastal%20erosion%20and%20threaten%20Ramsar-listed%20wetlands%20in%20the%20largest%20Great%20Barrier%20Reef%20watershed.%20%26lt%3Bi%26gt%3BEcohydrology%20%26amp%3B%20Hydrobiology%26lt%3B%5C%2Fi%26gt%3B%2C%20S1642359322000015.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecohyd.2022.01.001%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecohyd.2022.01.001%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Dams%20and%20climate%20change%20accelerate%20channel%20avulsion%20and%20coastal%20erosion%20and%20threaten%20Ramsar-listed%20wetlands%20in%20the%20largest%20Great%20Barrier%20Reef%20watershed%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Wolanski%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Christopher%22%2C%22lastName%22%3A%22Hopper%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221%5C%2F2022%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ecohyd.2022.01.001%22%2C%22ISSN%22%3A%2216423593%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS1642359322000015%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222022-01-23T15%3A03%3A11Z%22%7D%7D%2C%7B%22key%22%3A%22JXNVVP3L%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Figueiredo%20et%20al.%22%2C%22parsedDate%22%3A%222022%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BFigueiredo%2C%20J.%2C%20Thomas%2C%20C.%20J.%2C%20Deleersnijder%2C%20E.%2C%20Lambrechts%2C%20J.%2C%20Baird%2C%20A.%20H.%2C%20Connolly%2C%20S.%20R.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282022%29.%20Global%20warming%20decreases%20connectivity%20among%20coral%20populations.%20%26lt%3Bi%26gt%3BNature%20Climate%20Change%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B12%26lt%3B%5C%2Fi%26gt%3B%281%29%2C%2083%26%23x2013%3B87.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1038%5C%2Fs41558-021-01248-7%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1038%5C%2Fs41558-021-01248-7%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Global%20warming%20decreases%20connectivity%20among%20coral%20populations%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Joana%22%2C%22lastName%22%3A%22Figueiredo%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Christopher%20J.%22%2C%22lastName%22%3A%22Thomas%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Andrew%20H.%22%2C%22lastName%22%3A%22Baird%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sean%20R.%22%2C%22lastName%22%3A%22Connolly%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%2201%5C%2F2022%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1038%5C%2Fs41558-021-01248-7%22%2C%22ISSN%22%3A%221758-678X%2C%201758-6798%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.nature.com%5C%2Farticles%5C%2Fs41558-021-01248-7%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222022-02-06T10%3A42%3A17Z%22%7D%7D%2C%7B%22key%22%3A%226F7UHWTC%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Le%20et%20al.%22%2C%22parsedDate%22%3A%222020-08-27%22%2C%22numChildren%22%3A3%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BLe%2C%20H.-A.%2C%20Lambrechts%2C%20J.%2C%20Deleersnijder%2C%20E.%2C%20Soares-Frazao%2C%20S.%2C%20Gratiot%2C%20N.%2C%20Ortleb%2C%20S.%2C%20%26amp%3B%20Deleersnijder%2C%20E.%20%282020%29.%20Numerical%20modelling%20of%20flow%20dynamics%20in%20the%20Tonle%20Sap%20by%20means%20of%20a%20discontinuous%20Galerkin%20finite-element%20model.%20In%20W.%20Uijttewaal%2C%20M.%20J.%20Franca%2C%20D.%20Valero%2C%20V.%20Chavarrias%2C%20C.%20Ylla%20Arb%26%23xF3%3Bs%2C%20R.%20Schielen%2C%20%26amp%3B%20A.%20Crosato%20%28Eds.%29%2C%20%26lt%3Bi%26gt%3BRiver%20Flow%202020%26lt%3B%5C%2Fi%26gt%3B%20%281st%20ed.%2C%20pp.%201148%26%23x2013%3B1154%29.%20CRC%20Press.%20https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1201%5C%2Fb22619-160%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22bookSection%22%2C%22title%22%3A%22Numerical%20modelling%20of%20flow%20dynamics%20in%20the%20Tonle%20Sap%20by%20means%20of%20a%20discontinuous%20Galerkin%20finite-element%20model%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22editor%22%2C%22firstName%22%3A%22Wim%22%2C%22lastName%22%3A%22Uijttewaal%22%7D%2C%7B%22creatorType%22%3A%22editor%22%2C%22firstName%22%3A%22M%5Cu00e1rio%22%2C%22lastName%22%3A%22J.%20Franca%22%7D%2C%7B%22creatorType%22%3A%22editor%22%2C%22firstName%22%3A%22Daniel%22%2C%22lastName%22%3A%22Valero%22%7D%2C%7B%22creatorType%22%3A%22editor%22%2C%22firstName%22%3A%22Victor%22%2C%22lastName%22%3A%22Chavarrias%22%7D%2C%7B%22creatorType%22%3A%22editor%22%2C%22firstName%22%3A%22Cl%5Cu00e0udia%22%2C%22lastName%22%3A%22Ylla%20Arb%5Cu00f3s%22%7D%2C%7B%22creatorType%22%3A%22editor%22%2C%22firstName%22%3A%22Ralph%22%2C%22lastName%22%3A%22Schielen%22%7D%2C%7B%22creatorType%22%3A%22editor%22%2C%22firstName%22%3A%22Alessandra%22%2C%22lastName%22%3A%22Crosato%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Hoang-Anh%22%2C%22lastName%22%3A%22Le%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sandra%22%2C%22lastName%22%3A%22Soares-Frazao%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Nicolas%22%2C%22lastName%22%3A%22Gratiot%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sigrun%22%2C%22lastName%22%3A%22Ortleb%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22The%20Tonle%20Sap%20lake%2C%20located%20in%20the%20Cambodian%20floodplain%20of%20the%20Mekong%20River%20system%2C%20plays%20an%20important%20role%20for%20freshwater%20storage%20in%20Cambodia%20and%20the%20Vietnam%20Mekong%20Delta.%20The%20lake%5Cu2019s%20water%20level%20can%20rise%20by%20approximately%2010%20m%20and%20its%20water%20volume%20can%20increase%205%20times%20during%20a%20year%2C%20showing%20various%20drying%20and%20wetting%20areas%20in%20the%20lake%20and%20its%20floodplains.%20Thus%20the%20accurate%20simulation%20of%20wetting%20-%20drying%20processes%20in%20this%20domain%20is%20essential%20for%20water%20management%20in%20the%20Mekong%20River%20system.%20Here%2C%20we%20present%20the%20extension%20of%20an%20existing%20wetting%20-%20drying%20algorithm%20in%20two%20space%20dimensions.%20The%20algorithm%20consists%20in%20applying%20a%20threshold%20value%20of%20fluid%20depth%20for%20a%20thin%20layer%20and%20a%20blending%20parameter%20in%20order%20to%20guarantee%20positive%20values%20of%20the%20water%20depth%2C%20while%20preserving%20local%20mass%20conservation%20and%20the%20well-balanced%20property%20at%20wet%5C%2Fdry%20interfaces.%20It%20is%20implemented%20in%20SLIM%20%28Second-generation%20Louvain-la-Neuve%20Ice-ocean%20Model%2C%20www.%20slim-ocean.be%29%2C%20a%20discontinuous%20Galerkin%20finite%20element%20model%20%28DG-FEM%29%20solving%20the%20shallow%20water%20equations%20in%20a%20fully%20implicit%20way.%20Before%20applying%20in%20the%20Tonle%20Sap%20lake%2C%20the%20technique%20is%20validated%20against%20the%20standard%20analytical%20test%20cases%20%28Balzano%201%2C%20Balzano%203%20and%20Thacker%29.%22%2C%22bookTitle%22%3A%22River%20Flow%202020%22%2C%22date%22%3A%222020-8-27%22%2C%22language%22%3A%22en%22%2C%22ISBN%22%3A%22978-1-00-311095-8%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.taylorfrancis.com%5C%2Fbooks%5C%2F9781000294361%5C%2Fchapters%5C%2F10.1201%5C%2Fb22619-160%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222021-07-14T07%3A03%3A47Z%22%7D%7D%2C%7B%22key%22%3A%224U6RT34F%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Frys%20et%20al.%22%2C%22parsedDate%22%3A%222020-05-07%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BFrys%2C%20C.%2C%20Saint-Amand%2C%20A.%2C%20Le%20H%26%23xE9%3Bnaff%2C%20M.%2C%20Figueiredo%2C%20J.%2C%20Kuba%2C%20A.%2C%20Walker%2C%20B.%2C%20Lambrechts%2C%20J.%2C%20Vallaeys%2C%20V.%2C%20Vincent%2C%20D.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282020%29.%20Fine-Scale%20Coral%20Connectivity%20Pathways%20in%20the%20Florida%20Reef%20Tract%3A%20Implications%20for%20Conservation%20and%20Restoration.%20%26lt%3Bi%26gt%3BFrontiers%20in%20Marine%20Science%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B7%26lt%3B%5C%2Fi%26gt%3B.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.3389%5C%2Ffmars.2020.00312%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.3389%5C%2Ffmars.2020.00312%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Fine-Scale%20Coral%20Connectivity%20Pathways%20in%20the%20Florida%20Reef%20Tract%3A%20Implications%20for%20Conservation%20and%20Restoration%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Charles%22%2C%22lastName%22%3A%22Frys%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Antoine%22%2C%22lastName%22%3A%22Saint-Amand%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Matthieu%22%2C%22lastName%22%3A%22Le%20H%5Cu00e9naff%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Joana%22%2C%22lastName%22%3A%22Figueiredo%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Alyson%22%2C%22lastName%22%3A%22Kuba%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Brian%22%2C%22lastName%22%3A%22Walker%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Valentin%22%2C%22lastName%22%3A%22Vallaeys%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22David%22%2C%22lastName%22%3A%22Vincent%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222020-5-7%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.3389%5C%2Ffmars.2020.00312%22%2C%22ISSN%22%3A%222296-7745%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.frontiersin.org%5C%2Farticle%5C%2F10.3389%5C%2Ffmars.2020.00312%5C%2Ffull%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222020-05-07T06%3A59%3A26Z%22%7D%7D%2C%7B%22key%22%3A%22KHSUL6VK%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Le%20et%20al.%22%2C%22parsedDate%22%3A%222020-01-08%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BLe%2C%20H.-A.%2C%20Lambrechts%2C%20J.%2C%20Ortleb%2C%20S.%2C%20Gratiot%2C%20N.%2C%20Deleersnijder%2C%20E.%2C%20%26amp%3B%20Soares-Fraz%26%23xE3%3Bo%2C%20S.%20%282020%29.%20An%20implicit%20wetting%26%23x2013%3Bdrying%20algorithm%20for%20the%20discontinuous%20Galerkin%20method%3A%20application%20to%20the%20Tonle%20Sap%2C%20Mekong%20River%20Basin.%20%26lt%3Bi%26gt%3BEnvironmental%20Fluid%20Mechanics%26lt%3B%5C%2Fi%26gt%3B.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10652-019-09732-7%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10652-019-09732-7%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22An%20implicit%20wetting%5Cu2013drying%20algorithm%20for%20the%20discontinuous%20Galerkin%20method%3A%20application%20to%20the%20Tonle%20Sap%2C%20Mekong%20River%20Basin%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Hoang-Anh%22%2C%22lastName%22%3A%22Le%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sigrun%22%2C%22lastName%22%3A%22Ortleb%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Nicolas%22%2C%22lastName%22%3A%22Gratiot%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sandra%22%2C%22lastName%22%3A%22Soares-Fraz%5Cu00e3o%22%7D%5D%2C%22abstractNote%22%3A%22The%20accurate%20simulation%20of%20wetting%5Cu2013drying%20processes%20in%20%5Cufb02oodplains%20and%20coastal%20zones%20is%20a%20challenge%20for%20hydrodynamic%20modelling%2C%20especially%20for%20long%20time%20simulations.%20Indeed%2C%20dedicated%20numerical%20procedures%20are%20generally%20time-consuming%2C%20instabilities%20can%20occur%20at%20the%20wet%5C%2Fdry%20front%2C%20rapid%20transition%20of%20wet%5C%2Fdry%20interface%20and%20mass%20conservation%20are%20not%20always%20ensured.%20We%20present%20the%20extension%20of%20an%20existing%20wetting%5Cu2013drying%20algorithm%20in%20two%20space%20dimensions%20and%20its%20application%20to%20a%20real%20case.%20The%20wetting%5Cu2013drying%20algorithm%20is%20implemented%20in%20Second-generation%20Louvain-la-Neuve%20Ice-ocean%20Model%20%28www.slim-ocean.be%29%2C%20a%20discontinuous%20Galerkin%20%5Cufb01nite%20element%20model%20solving%20the%20shallow%20water%20equations%20in%20a%20fully%20implicit%20way.%20This%20algorithm%20consists%20in%20applying%20a%20threshold%20value%20of%20%5Cufb02uid%20depth%20for%20a%20thin%20layer%20and%20a%20blending%20parameter%20in%20order%20to%20guarantee%20positive%20values%20of%20the%20water%20depth%2C%20while%20preserving%20local%20mass%20conservation%20and%20the%20well%20balanced%20property%20at%20wet%5C%2Fdry%20interfaces.%20The%20technique%20is%20%5Cufb01rst%20validated%20against%20standard%20analytical%20test%20cases%20%28Balzano%201%2C%20Balzano%203%20and%20Thacker%20test%20cases%29%20and%20is%20subsquently%20applied%20in%20a%20realistic%20domain%2C%20the%20Tonle%20Sap%20Lake%20in%20the%20Mekong%20River%20Basin%2C%20where%20the%20water%20level%20can%20vary%20by%20about%2010%20m%20between%20the%20dry%20and%20the%20wet%20season.%22%2C%22date%22%3A%222020-1-8%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs10652-019-09732-7%22%2C%22ISSN%22%3A%221567-7419%2C%201573-1510%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs10652-019-09732-7%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222020-01-14T16%3A33%3A36Z%22%7D%7D%2C%7B%22key%22%3A%2228VULX74%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Le%20et%20al.%22%2C%22parsedDate%22%3A%222020%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BLe%2C%20H.-A.%2C%20Gratiot%2C%20N.%2C%20Santini%2C%20W.%2C%20Ribolzi%2C%20O.%2C%20Tran%2C%20D.%2C%20Meriaux%2C%20X.%2C%20Deleersnijder%2C%20E.%2C%20%26amp%3B%20Soares-Fraz%26%23xE3%3Bo%2C%20S.%20%282020%29.%20Suspended%20sediment%20properties%20in%20the%20Lower%20Mekong%20River%2C%20from%20fluvial%20to%20estuarine%20environments.%20%26lt%3Bi%26gt%3BEstuarine%2C%20Coastal%20and%20Shelf%20Science%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B233%26lt%3B%5C%2Fi%26gt%3B%2C%20106522.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecss.2019.106522%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecss.2019.106522%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Suspended%20sediment%20properties%20in%20the%20Lower%20Mekong%20River%2C%20from%20fluvial%20to%20estuarine%20environments%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Hoang-Anh%22%2C%22lastName%22%3A%22Le%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Nicolas%22%2C%22lastName%22%3A%22Gratiot%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22William%22%2C%22lastName%22%3A%22Santini%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Olivier%22%2C%22lastName%22%3A%22Ribolzi%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Duc%22%2C%22lastName%22%3A%22Tran%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Xavier%22%2C%22lastName%22%3A%22Meriaux%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sandra%22%2C%22lastName%22%3A%22Soares-Fraz%5Cu00e3o%22%7D%5D%2C%22abstractNote%22%3A%22The%20Mekong%20river%20is%20one%20of%20the%20largest%20rivers%20in%20the%20world%2C%20which%20flows%20through%20six%20countries%20of%20Southeast%20Asia%20%28China%2C%20Myanmar%2C%20Laos%2C%20Thailand%2C%20Cambodia%20and%20Vietnam%29.%20Its%20hydro-sedimentary%20regime%20is%20changing%20rapidly%2C%20as%20a%20consequence%20of%20a%20regional%20shift%20of%20land%20use%20%28agriculture%2C%20road%2C%20etc.%29%2C%20damming%2C%20sand%20mining%20and%20climate%20changes%2C%20among%20others.%20This%20study%20assesses%20the%20behavior%20of%20particles%20transported%20in%20suspension%20in%20the%20Lower%20Mekong%20River%20%28LMR%29%2C%20along%20approximately%201700%20km%20from%20fluvial%20to%20estuarine%20environments.%20Suspended%20sediment%20properties%20were%20estimated%2C%20simultaneously%20with%20hydrodynamic%20conditions%2C%20during%20three%20field%20campaigns.%20In%20addition%2C%20further%20investigations%20were%20performed%20in%20the%20laboratory%20to%20assess%20the%20structures%20of%20particles%20%28flocculated%20or%20not%29%2C%20their%20capacity%20to%20flocculate%20%28and%20the%20impacts%20on%20siltation%29%2C%20under%20a%20wide%20range%20of%20sediment%20concentration%20%2820%5Cu201330%2C000%20mg.L%201%29.%20This%20study%20confirms%20that%20suspended%20sediment%20transported%20in%20the%20LMR%20are%20predominantly%20%2875%25%20by%20volume%29%20flocculi%20%28or%20freshly%20eroded%20soils%20aggregates%29%2C%20with%20median%20aggregated%20particle%20size%20in%20the%20range%2010%5Cu201320%20%5Cu03bcm%20and%20median%20settling%20velocity%20of%20the%20order%20of%200.01%5Cu20130.1%20mm%20s%201.%20These%20flocculi%20are%20robust%20under%20the%20hydrodynamic%20conditions%20%28turbulence%20and%20suspended%20sediment%20concentration%20%5Cu2013%20SSC%29%20existing%20in%20the%20LMR.%20Lab%5Cu00ad%20oratory%20investigations%20reveal%20the%20existence%20of%20a%20threshold%20sediment%20concentration%20%28400%20mg.L%201%29%2C%20beyond%20which%20flocculation%20and%20sedimentation%20increase%20of%20orders%20of%20magnitudes.%20Thus%2C%20concentration%20that%20exceeds%20this%20threshold%20might%20promote%20the%20formation%20of%20so-called%20fluid%20mud%20layers.%20Because%20of%20the%20nonlinear%20response%20of%20flocculation%20and%20sedimentation%20with%20SSC%20and%20considering%20the%20ongoing%20changes%20at%20a%20regional%20scale%20in%20the%20LMR%2C%20higher%20occurrence%20of%20fluid%20mud%20layers%20in%20the%20fluvial%20upstream%20waterbodies%20might%20be%20anticipated%2C%20and%20a%20lower%20occurrence%20in%20estuaries%20and%20alongshore%20where%20the%20concentration%20decrease.%20The%20geomorphology%20could%20be%20impacted%2C%20with%20an%20over-siltation%20in%20dams%20and%20an%20exacerbated%20erosion%20of%20the%20muddy-mangrove%20coast.%22%2C%22date%22%3A%2202%5C%2F2020%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ecss.2019.106522%22%2C%22ISSN%22%3A%2202727714%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0272771419306171%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222020-01-14T16%3A33%3A28Z%22%7D%7D%2C%7B%22key%22%3A%227E8RMW74%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Dobbelaere%20et%20al.%22%2C%22parsedDate%22%3A%222020%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BDobbelaere%2C%20T.%2C%20Muller%2C%20Erinn%2C%20Gramer%2C%20Lewis%2C%20Holstein%2C%20Daniel%2C%20%26amp%3B%20Hanert%2C%20E.%20%282020%29.%20Coupled%20Epidemio-Hydrodynamic%20Modeling%20to%20Understand%20the%20Spread%20of%20a%20Deadly%20Coral%20Disease%20in%20Florida.%20%26lt%3Bi%26gt%3BFrontiers%20in%20Marine%20Science%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B7%26lt%3B%5C%2Fi%26gt%3B%2C%2016.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.3389%5C%2Ffmars.2020.591881%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.3389%5C%2Ffmars.2020.591881%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Coupled%20Epidemio-Hydrodynamic%20Modeling%20to%20Understand%20the%20Spread%20of%20a%20Deadly%20Coral%20Disease%20in%20Florida%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Dobbelaere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%22%2C%22lastName%22%3A%22Muller%2C%20Erinn%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%22%2C%22lastName%22%3A%22Gramer%2C%20Lewis%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%22%2C%22lastName%22%3A%22Holstein%2C%20Daniel%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%222020%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.3389%5C%2Ffmars.2020.591881%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.frontiersin.org%5C%2Farticles%5C%2F10.3389%5C%2Ffmars.2020.591881%5C%2Ffull%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222020-12-13T14%3A10%3A22Z%22%7D%7D%2C%7B%22key%22%3A%22TPVAGHVG%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Vincent%20et%20al.%22%2C%22parsedDate%22%3A%222019-08-31%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BVincent%2C%20D.%2C%20Lambrechts%2C%20J.%2C%20Karatekin%2C%20%26%23xD6%3B.%2C%20Van%20Hoolst%2C%20T.%2C%20Tyler%2C%20R.%20H.%2C%20Dehant%2C%20V.%2C%20%26amp%3B%20Deleersnijder%2C%20E.%20%282019%29.%20Normal%20modes%20and%20resonance%20in%20Ontario%20Lacus%3A%20a%20hydrocarbon%20lake%20of%20Titan.%20%26lt%3Bi%26gt%3BOcean%20Dynamics%26lt%3B%5C%2Fi%26gt%3B.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-019-01290-2%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-019-01290-2%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Normal%20modes%20and%20resonance%20in%20Ontario%20Lacus%3A%20a%20hydrocarbon%20lake%20of%20Titan%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22David%22%2C%22lastName%22%3A%22Vincent%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%5Cu00d6zg%5Cu00fcr%22%2C%22lastName%22%3A%22Karatekin%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Tim%22%2C%22lastName%22%3A%22Van%20Hoolst%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Robert%20H.%22%2C%22lastName%22%3A%22Tyler%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22V%5Cu00e9ronique%22%2C%22lastName%22%3A%22Dehant%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22The%20natural%20modes%20of%20Ontario%20Lacus%20surface%20oscillations%2C%20the%20largest%20lake%20in%20Titan%5Cu2019s%20southern%20hemisphere%2C%20are%20simulated%20and%20analyzed%20as%20they%20are%20potentially%20of%20broad%20interest%20in%20a%20variety%20of%20dynamical%20researches.%20We%20found%20that%20tidal%20forces%20are%20too%20low%20in%20frequency%20to%20excite%20the%20%28barotropic%29%20normal%20modes.%20Broadband%20wind%20forcing%20likely%20spans%20the%20resonant%20frequencies.%20High%20wind%20speed%2C%20which%20could%20be%20encountered%20under%20episodic%20phenomena%20such%20as%20storms%2C%20would%20be%20required%20to%20significantly%20excite%20the%20normal%20modes.%20While%20the%20slower%20baroclinic%20normal%20modes%20could%20more%20easily%20be%20resonantly%20forced%20by%20the%20low-frequency%20tidal%20forces%2C%20addressing%20this%20issue%20demands%20unavailable%20information%20about%20the%20lake%20stratification.%22%2C%22date%22%3A%222019-8-31%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs10236-019-01290-2%22%2C%22ISSN%22%3A%221616-7341%2C%201616-7228%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs10236-019-01290-2%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-03-07T18%3A59%3A30Z%22%7D%7D%2C%7B%22key%22%3A%222PE5KVFJ%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Vincent%20et%20al.%22%2C%22parsedDate%22%3A%222018%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BVincent%2C%20D.%2C%20Karatekin%2C%20%26%23xD6%3B.%2C%20Lambrechts%2C%20J.%2C%20Lorenz%2C%20R.%20D.%2C%20Dehant%2C%20V.%2C%20%26amp%3B%20Deleersnijder%2C%20%26%23xC9%3B.%20%282018%29.%20A%20numerical%20study%20of%20tides%20in%20Titan%26%23x2032%3Bs%20northern%20seas%2C%20Kraken%20and%20Ligeia%20Maria.%20%26lt%3Bi%26gt%3BIcarus%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B310%26lt%3B%5C%2Fi%26gt%3B%2C%20105%26%23x2013%3B126.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.icarus.2017.12.018%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.icarus.2017.12.018%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20numerical%20study%20of%20tides%20in%20Titan%5Cu2032s%20northern%20seas%2C%20Kraken%20and%20Ligeia%20Maria%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22David%22%2C%22lastName%22%3A%22Vincent%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%5Cu00d6zg%5Cu00fcr%22%2C%22lastName%22%3A%22Karatekin%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ralph%20D.%22%2C%22lastName%22%3A%22Lorenz%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22V%5Cu00e9ronique%22%2C%22lastName%22%3A%22Dehant%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%5Cu00c9ric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22The%20tidal%20response%20of%20Titan%20s%20two%20largest%20northern%20seas%2C%20Ligeia%20Mare%20and%20Kraken%20Mare%2C%20is%20studied%20by%20means%20of%20a%20two-dimensional%2C%20depth-averaged%2C%20shallow%20water%20model%2C%20SLIM%20%28http%3A%5C%2F%5C%2Fwww.climate.be%5C%2Fslim%29.%20Kraken%20Mare%20is%20formed%20of%20two%20basins%2C%20the%20northern%20one%20being%20assumed%20to%20be%20linked%20by%20a%20single%20strait%2C%20Trevize%20Fretum%2C%20to%20Ligeia%20Mare.%20The%20tidal%20motions%20tend%20to%20be%20independent%20of%20each%20other%20in%20each%20basin%20%28i.e.%2C%20Ligeia%20Mare%2C%20Kraken%201%20and%20Kraken%202%29%20which%20results%20in%20sharp%20transitions%20in%20the%20straits.%20Our%20results%20are%20overall%20rather%20similar%20to%20those%20of%20Tokano%20et%20al.%20%282014%29%2C%20suggesting%20that%20a%202D%20model%20such%20as%20SLIM%20is%20adequate%20for%20modelling%20Titan%20s%20tides%20and%2C%20since%20it%20is%20%28presumably%29%20less%20computationally%20demanding%2C%20may%20be%20better%20for%20sensitivity%20studies.%20For%20instance%2C%20the%20maximum%20tidal%20range%20in%20Kraken%20and%20Ligeia%20Maria%20respectively%20are%200.29%20m%20and%200.14%20m%2C%20which%20is%20within%20the%20range%20predicted%20by%20Lorenz%20et%20al.%20%282014%29%20although%20smaller%20by%200.07%20m%20and%20larger%20by%200.04%20m%20than%20the%20estimates%20of%20Tokano%20et%20al.%20%282014%29%20%28but%20it%20occurs%20at%20the%20same%20location%29.%20The%20tidal%20currents%20are%20faster%20%28by%20about%20one%20order%20of%20magnitude%29%20in%20the%20straits%20linking%20those%20Maria%20than%20in%20the%20basins%20themselves%20%28with%20a%20maximum%20of%200.36%20m%5C%2Fs%20in%20the%20strait%20linking%20Kraken%201%20and%20Kraken%202%2C%20Seldon%20Fretum%29.%20A%20decomposition%20of%20the%20tidal%20history%20into%20different%20harmonic%20components%20is%20carried%20out.%20Except%20in%20speci%5Cufb01c%20areas%20such%20as%20the%20straits%20and%20the%20amphidromic%20point%28s%29%2C%20the%20main%20tidal%20component%20has%20a%20period%20of%201%20Titan%20Day.%20We%20also%20brie%5Cufb02y%20studied%20the%20eigenmodes%20of%20the%20northern%20seas%20whose%20period%20is%20close%20to%20the%20tidal%20period%3A%20such%20modes%20are%20very%20local.%20Indeed%2C%20their%20magnitude%20is%20signi%5Cufb01cant%20%28with%20respect%20to%20the%20magnitude%20of%20the%20modes%20elsewhere%20in%20the%20seas%29%20in%20small%20bay%28s%29%20or%20near%20the%20islands%20of%20Kraken%202%20and%20Ligeia%20Mare.%20They%20are%20not%20excited%20by%20the%20tides%20as%20they%20do%20not%20appear%20in%20the%20tidal%20motion.%22%2C%22date%22%3A%2208%5C%2F2018%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.icarus.2017.12.018%22%2C%22ISSN%22%3A%2200191035%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0019103517305055%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A57%3A42Z%22%7D%7D%2C%7B%22key%22%3A%228EC6CIL2%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Delandmeter%20et%20al.%22%2C%22parsedDate%22%3A%222017%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BDelandmeter%2C%20P.%2C%20Lambrechts%2C%20J.%2C%20Marmorino%2C%20G.%20O.%2C%20Legat%2C%20V.%2C%20Wolanski%2C%20E.%2C%20Remacle%2C%20J.-F.%2C%20Chen%2C%20W.%2C%20%26amp%3B%20Deleersnijder%2C%20E.%20%282017%29.%20Submesoscale%20tidal%20eddies%20in%20the%20wake%20of%20coral%20islands%20and%20reefs%3A%20satellite%20data%20and%20numerical%20modelling.%20%26lt%3Bi%26gt%3BOcean%20Dynamics%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B67%26lt%3B%5C%2Fi%26gt%3B%287%29%2C%20897%26%23x2013%3B913.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-017-1066-z%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-017-1066-z%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Submesoscale%20tidal%20eddies%20in%20the%20wake%20of%20coral%20islands%20and%20reefs%3A%20satellite%20data%20and%20numerical%20modelling%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Philippe%22%2C%22lastName%22%3A%22Delandmeter%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22George%20O.%22%2C%22lastName%22%3A%22Marmorino%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Wolanski%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jean-Fran%5Cu00e7ois%22%2C%22lastName%22%3A%22Remacle%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Wei%22%2C%22lastName%22%3A%22Chen%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%227%5C%2F2017%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs10236-017-1066-z%22%2C%22ISSN%22%3A%221616-7341%2C%201616-7228%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs10236-017-1066-z%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A51%3A41Z%22%7D%7D%2C%7B%22key%22%3A%225K8MRRSH%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Pham%20Van%20et%20al.%22%2C%22parsedDate%22%3A%222016%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BPham%20Van%2C%20C.%2C%20de%20Brye%2C%20B.%2C%20Deleersnijder%2C%20E.%2C%20Hoitink%2C%20A.%20J.%20F.%2C%20Sassi%2C%20M.%2C%20Spinewine%2C%20B.%2C%20Hidayat%2C%20H.%2C%20%26amp%3B%20Soares-Fraz%26%23xE3%3Bo%2C%20S.%20%282016%29.%20Simulations%20of%20the%20flow%20in%20the%20Mahakam%20river%26%23x2013%3Blake%26%23x2013%3Bdelta%20system%2C%20Indonesia.%20%26lt%3Bi%26gt%3BEnvironmental%20Fluid%20Mechanics%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B16%26lt%3B%5C%2Fi%26gt%3B%283%29%2C%20603%26%23x2013%3B633.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10652-016-9445-4%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10652-016-9445-4%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Simulations%20of%20the%20flow%20in%20the%20Mahakam%20river%5Cu2013lake%5Cu2013delta%20system%2C%20Indonesia%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Chien%22%2C%22lastName%22%3A%22Pham%20Van%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Benjamin%22%2C%22lastName%22%3A%22de%20Brye%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22A.%20J.%20F.%22%2C%22lastName%22%3A%22Hoitink%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Maximiliano%22%2C%22lastName%22%3A%22Sassi%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Benoit%22%2C%22lastName%22%3A%22Spinewine%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Hidayat%22%2C%22lastName%22%3A%22Hidayat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Sandra%22%2C%22lastName%22%3A%22Soares-Fraz%5Cu00e3o%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%226%5C%2F2016%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs10652-016-9445-4%22%2C%22ISSN%22%3A%221567-7419%2C%201573-1510%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs10652-016-9445-4%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-03-06T09%3A30%3A21Z%22%7D%7D%2C%7B%22key%22%3A%22A37KES8N%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Vincent%20et%20al.%22%2C%22parsedDate%22%3A%222016%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BVincent%2C%20D.%2C%20Karatekin%2C%20%26%23xD6%3B.%2C%20Vallaeys%2C%20V.%2C%20Hayes%2C%20A.%20G.%2C%20Mastrogiuseppe%2C%20M.%2C%20Notarnicola%2C%20C.%2C%20Dehant%2C%20V.%2C%20%26amp%3B%20Deleersnijder%2C%20E.%20%282016%29.%20Numerical%20study%20of%20tides%20in%20Ontario%20Lacus%2C%20a%20hydrocarbon%20lake%20on%20the%20surface%20of%20the%20Saturnian%20moon%20Titan.%20%26lt%3Bi%26gt%3BOcean%20Dynamics%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B66%26lt%3B%5C%2Fi%26gt%3B%284%29%2C%20461%26%23x2013%3B482.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-016-0926-2%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-016-0926-2%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Numerical%20study%20of%20tides%20in%20Ontario%20Lacus%2C%20a%20hydrocarbon%20lake%20on%20the%20surface%20of%20the%20Saturnian%20moon%20Titan%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22David%22%2C%22lastName%22%3A%22Vincent%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%5Cu00d6zgur%22%2C%22lastName%22%3A%22Karatekin%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Valentin%22%2C%22lastName%22%3A%22Vallaeys%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Alexander%20G.%22%2C%22lastName%22%3A%22Hayes%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Marco%22%2C%22lastName%22%3A%22Mastrogiuseppe%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Claudia%22%2C%22lastName%22%3A%22Notarnicola%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22V%5Cu00e9ronique%22%2C%22lastName%22%3A%22Dehant%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%224%5C%2F2016%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs10236-016-0926-2%22%2C%22ISSN%22%3A%221616-7341%2C%201616-7228%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs10236-016-0926-2%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A57%3A48Z%22%7D%7D%2C%7B%22key%22%3A%22W95GT4DY%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Le%20Bars%20et%20al.%22%2C%22parsedDate%22%3A%222016%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BLe%20Bars%2C%20Y.%2C%20Vallaeys%2C%20V.%2C%20Deleersnijder%2C%20%26%23xC9%3B.%2C%20Hanert%2C%20E.%2C%20Carrere%2C%20L.%2C%20%26amp%3B%20Channeli%26%23xE8%3Bre%2C%20C.%20%282016%29.%20Unstructured-mesh%20modeling%20of%20the%20Congo%20river-to-sea%20continuum.%20%26lt%3Bi%26gt%3BOcean%20Dynamics%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B66%26lt%3B%5C%2Fi%26gt%3B%284%29%2C%20589%26%23x2013%3B603.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-016-0939-x%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-016-0939-x%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Unstructured-mesh%20modeling%20of%20the%20Congo%20river-to-sea%20continuum%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Yoann%22%2C%22lastName%22%3A%22Le%20Bars%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Valentin%22%2C%22lastName%22%3A%22Vallaeys%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%5Cu00c9ric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Loren%22%2C%22lastName%22%3A%22Carrere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Claire%22%2C%22lastName%22%3A%22Channeli%5Cu00e8re%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%224%5C%2F2016%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs10236-016-0939-x%22%2C%22ISSN%22%3A%221616-7341%2C%201616-7228%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs10236-016-0939-x%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A54%3A43Z%22%7D%7D%2C%7B%22key%22%3A%22ADTT9IX6%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Thomas%20et%20al.%22%2C%22parsedDate%22%3A%222014%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BThomas%2C%20C.%20J.%2C%20Lambrechts%2C%20J.%2C%20Wolanski%2C%20E.%2C%20Traag%2C%20V.%20A.%2C%20Blondel%2C%20V.%20D.%2C%20Deleersnijder%2C%20E.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282014%29.%20Numerical%20modelling%20and%20graph%20theory%20tools%20to%20study%20ecological%20connectivity%20in%20the%20Great%20Barrier%20Reef.%20%26lt%3Bi%26gt%3BEcological%20Modelling%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B272%26lt%3B%5C%2Fi%26gt%3B%2C%20160%26%23x2013%3B174.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecolmodel.2013.10.002%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecolmodel.2013.10.002%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Numerical%20modelling%20and%20graph%20theory%20tools%20to%20study%20ecological%20connectivity%20in%20the%20Great%20Barrier%20Reef%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Christopher%20J.%22%2C%22lastName%22%3A%22Thomas%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Wolanski%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%20A.%22%2C%22lastName%22%3A%22Traag%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%20D.%22%2C%22lastName%22%3A%22Blondel%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22The%20process%20of%20coral%20larval%20dispersal%20is%20important%20for%20coral%20reef%20ecosystems%2C%20but%20remains%20poorly%20understood%20and%20hard%20to%20gauge.%20Better%20knowledge%20of%20inter-reef%20connectivity%20patterns%20would%20be%20useful%20in%20enabling%20better%20management%20of%20coral%20reef%20waters%20however.%20By%20employing%20a%20spatially%20explicit%20numerical%20modelling%20approach%2C%20we%20simulate%20larval%20dispersal%20through%20the%20central%20section%20of%20the%20Great%20Barrier%20Reef%20%28GBR%29%2C%20comprising%20over%201000%20reefs%2C%20and%20identify%20spatial%20patterns%20in%20the%20inter-reef%20connectivity%20network%20using%20a%20community%20detection%20method%20from%20network%20science.%20This%20paper%20presents%20the%20modelling%20approach%20used%20and%20discusses%20the%20signi%5Cufb01cance%20of%20the%20results.%22%2C%22date%22%3A%2201%5C%2F2014%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ecolmodel.2013.10.002%22%2C%22ISSN%22%3A%2203043800%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS030438001300464X%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A57%3A23Z%22%7D%7D%2C%7B%22key%22%3A%22BRPEQMIJ%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22lastModifiedByUser%22%3A%7B%22id%22%3A5103066%2C%22username%22%3A%22ehanert%22%2C%22name%22%3A%22%22%2C%22links%22%3A%7B%22alternate%22%3A%7B%22href%22%3A%22https%3A%5C%2F%5C%2Fwww.zotero.org%5C%2Fehanert%22%2C%22type%22%3A%22text%5C%2Fhtml%22%7D%7D%7D%2C%22creatorSummary%22%3A%22K%5Cu00e4rn%5Cu00e4%20et%20al.%22%2C%22parsedDate%22%3A%222011-01-15%22%2C%22numChildren%22%3A4%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BK%26%23xE4%3Brn%26%23xE4%3B%2C%20T.%2C%20de%20Brye%2C%20B.%2C%20Gourgue%2C%20O.%2C%20Lambrechts%2C%20J.%2C%20Comblen%2C%20R.%2C%20Legat%2C%20V.%2C%20%26amp%3B%20Deleersnijder%2C%20E.%20%282011%29.%20A%20fully%20implicit%20wetting%26%23x2013%3Bdrying%20method%20for%20DG-FEM%20shallow%20water%20models%2C%20with%20an%20application%20to%20the%20Scheldt%20Estuary.%20%26lt%3Bi%26gt%3BComputer%20Methods%20in%20Applied%20Mechanics%20and%20Engineering%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B200%26lt%3B%5C%2Fi%26gt%3B%285%26%23x2013%3B8%29%2C%20509%26%23x2013%3B524.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.cma.2010.07.001%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.cma.2010.07.001%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20fully%20implicit%20wetting%5Cu2013drying%20method%20for%20DG-FEM%20shallow%20water%20models%2C%20with%20an%20application%20to%20the%20Scheldt%20Estuary%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Tuomas%22%2C%22lastName%22%3A%22K%5Cu00e4rn%5Cu00e4%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Benjamin%22%2C%22lastName%22%3A%22de%20Brye%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Olivier%22%2C%22lastName%22%3A%22Gourgue%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%22%2C%22lastName%22%3A%22Comblen%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22Resolving%20the%20shoreline%20undulation%20due%20to%20tidal%20excursion%20is%20a%20crucial%20part%20of%20modelling%20water%20flow%20in%20estuaries%20and%20coastal%20areas.%20Nevertheless%2C%20maintaining%20positive%20water%20column%20depth%20and%20numerical%20stability%20has%20proved%20out%20to%20be%20a%20very%20difficult%20task%20that%20requires%20special%20attention.%20In%20this%20paper%20we%20propose%20a%20novel%20wetting%5Cu2013drying%20method%20in%20which%20the%20position%20of%20the%20sea%20bed%20is%20allowed%20to%20fluctuate%20in%20drying%20areas.%20The%20method%20is%20implemented%20in%20a%20Discontinuous%20Galerkin%20Finite%20Element%20Model%20%28DG-FEM%29.%20Unlike%20most%20methods%20in%20the%20literature%20our%20method%20is%20compatible%20with%20fully%20implicit%20time-marching%20schemes%2C%20thus%20reducing%20the%20overall%20computational%20cost%20significantly.%20Moreover%2C%20global%20and%20local%20mass%20conservation%20is%20guaranteed%20which%20is%20crucial%20for%20long-term%20environmental%20applications.%20In%20addition%20consistency%20with%20tracer%20equation%20is%20also%20ensured.%20The%20performance%20of%20the%20proposed%20method%20is%20demonstrated%20with%20a%20set%20of%20test%20cases%20as%20well%20as%20a%20real-world%20application%20to%20the%20Scheldt%20Estuary.%20Due%20to%20the%20implicit%20time%20integration%2C%20the%20computational%20cost%20in%20the%20Scheldt%20application%20is%20reduced%20by%20two%20orders%20of%20magnitude.%20Although%20a%20DG-FEM%20implementation%20is%20presented%20here%2C%20the%20wetting%5Cu2013drying%20method%20is%20applicable%20to%20a%20wide%20variety%20of%20shallow%20water%20models.%22%2C%22date%22%3A%22January%2015%2C%202011%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.cma.2010.07.001%22%2C%22ISSN%22%3A%220045-7825%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fwww.sciencedirect.com%5C%2Fscience%5C%2Farticle%5C%2Fpii%5C%2FS0045782510002136%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%2C%227VXM6D4Z%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A53%3A34Z%22%7D%7D%2C%7B%22key%22%3A%22WB3C9LWG%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22de%20Brye%20et%20al.%22%2C%22parsedDate%22%3A%222011%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3Bde%20Brye%2C%20B.%2C%20Schellen%2C%20S.%2C%20Sassi%2C%20M.%2C%20Vermeulen%2C%20B.%2C%20K%26%23xE4%3Brn%26%23xE4%3B%2C%20T.%2C%20Deleersnijder%2C%20E.%2C%20%26amp%3B%20Hoitink%2C%20T.%20%282011%29.%20Preliminary%20results%20of%20a%20finite-element%2C%20multi-scale%20model%20of%20the%20Mahakam%20Delta%20%28Indonesia%29.%20%26lt%3Bi%26gt%3BOcean%20Dynamics%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B61%26lt%3B%5C%2Fi%26gt%3B%288%29%2C%201107%26%23x2013%3B1120.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-011-0410-y%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-011-0410-y%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Preliminary%20results%20of%20a%20finite-element%2C%20multi-scale%20model%20of%20the%20Mahakam%20Delta%20%28Indonesia%29%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Benjamin%22%2C%22lastName%22%3A%22de%20Brye%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22S%5Cu00e9bastien%22%2C%22lastName%22%3A%22Schellen%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Maximiliano%22%2C%22lastName%22%3A%22Sassi%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Bart%22%2C%22lastName%22%3A%22Vermeulen%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Tuomas%22%2C%22lastName%22%3A%22K%5Cu00e4rn%5Cu00e4%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ton%22%2C%22lastName%22%3A%22Hoitink%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%228%5C%2F2011%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs10236-011-0410-y%22%2C%22ISSN%22%3A%221616-7341%2C%201616-7228%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs10236-011-0410-y%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-03-06T09%3A30%3A25Z%22%7D%7D%2C%7B%22key%22%3A%22K7YKTE3E%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22de%20Brye%20et%20al.%22%2C%22parsedDate%22%3A%222010%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3Bde%20Brye%2C%20B.%2C%20de%20Brauwere%2C%20A.%2C%20Gourgue%2C%20O.%2C%20K%26%23xE4%3Brn%26%23xE4%3B%2C%20T.%2C%20Lambrechts%2C%20J.%2C%20Comblen%2C%20R.%2C%20%26amp%3B%20Deleersnijder%2C%20E.%20%282010%29.%20A%20finite-element%2C%20multi-scale%20model%20of%20the%20Scheldt%20tributaries%2C%20river%2C%20estuary%20and%20ROFI.%20%26lt%3Bi%26gt%3BCoastal%20Engineering%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B57%26lt%3B%5C%2Fi%26gt%3B%289%29%2C%20850%26%23x2013%3B863.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.coastaleng.2010.04.001%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.coastaleng.2010.04.001%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20finite-element%2C%20multi-scale%20model%20of%20the%20Scheldt%20tributaries%2C%20river%2C%20estuary%20and%20ROFI%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Benjamin%22%2C%22lastName%22%3A%22de%20Brye%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Anouk%22%2C%22lastName%22%3A%22de%20Brauwere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Olivier%22%2C%22lastName%22%3A%22Gourgue%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Tuomas%22%2C%22lastName%22%3A%22K%5Cu00e4rn%5Cu00e4%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%22%2C%22lastName%22%3A%22Comblen%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22We%20report%20on%20the%20development%20and%20validation%20of%20a%20coupled%20two-%20and%20one-dimensional%20%5Cufb01nite-element%20model%20for%20the%20Scheldt%20tributaries%2C%20river%2C%20estuary%20and%20region%20of%20fresh%20water%20in%5Cufb02uence%20%28ROFI%29.%20The%20hydrodynamic%20equations%20are%20solved%20on%20a%20single%2C%20unstructured%2C%20multi-scale%20mesh%20stretching%20from%20the%20shelf%20break%20to%20the%20Scheldt%20tributaries.%20The%20tide%20is%20forced%20on%20the%20shelf%20break%20and%20propagates%20upstream%20in%20the%20riverine%20network.%20Upstream%20boundaries%20lie%20on%20sluices%20or%20outside%20of%20the%20region%20of%20tidal%20dominance%20where%20daily%20averaged%20discharges%20are%20imposed.%20Two-dimensional%2C%20depth-averaged%20shallow%20water%20equations%20are%20solved%20by%20means%20of%20the%20discontinuous%20Galerkin%20%28DG%29%20method%20over%20the%20marine%20and%20estuarine%20parts%20of%20the%20computational%20domain.%20In%20the%20rivers%2C%20however%2C%20one-dimensional%20equations%20are%20dealt%20with%20using%20the%20DG%20method%20with%20the%20addition%20of%20a%20technique%20to%20cope%20with%20con%5Cufb02uence%20points.%20Model%20parameters%20are%20carefully%20calibrated%2C%20leading%20to%20the%20simulation%20of%20wind-%20and%20tide-forced%20%5Cufb02ows%20that%20are%20in%20excellent%20agreement%20with%20available%20data.%20The%20diffusivity%20in%20the%20transport%20equation%20is%20calibrated%20using%20time%20series%20of%20salinity%20at%20various%20locations%20in%20the%20estuary.%20Finally%2C%20the%20Lagrangian%20residual%20transport%20in%20the%20estuary%20and%20the%20adjacent%20coastal%20zone%20is%20investigated.%20This%20work%20is%20a%20major%20step%20towards%20an%20integrated%20model%20for%20studying%20the%20dynamics%20of%20waterborne%20contaminants%20and%20the%20water%20renewal%20timescales%20in%20the%20Scheldt%20land-sea%20continuum.%22%2C%22date%22%3A%229%5C%2F2010%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.coastaleng.2010.04.001%22%2C%22ISSN%22%3A%2203783839%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0378383910000487%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A49%3A54Z%22%7D%7D%2C%7B%22key%22%3A%226JCIRWUN%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22lastModifiedByUser%22%3A%7B%22id%22%3A5103066%2C%22username%22%3A%22ehanert%22%2C%22name%22%3A%22%22%2C%22links%22%3A%7B%22alternate%22%3A%7B%22href%22%3A%22https%3A%5C%2F%5C%2Fwww.zotero.org%5C%2Fehanert%22%2C%22type%22%3A%22text%5C%2Fhtml%22%7D%7D%7D%2C%22creatorSummary%22%3A%22Gourgue%20et%20al.%22%2C%22parsedDate%22%3A%222009-12%22%2C%22numChildren%22%3A5%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BGourgue%2C%20O.%2C%20Comblen%2C%20R.%2C%20Lambrechts%2C%20J.%2C%20K%26%23xE4%3Brn%26%23xE4%3B%2C%20T.%2C%20Legat%2C%20V.%2C%20%26amp%3B%20Deleersnijder%2C%20E.%20%282009%29.%20A%20flux-limiting%20wetting%26%23x2013%3Bdrying%20method%20for%20finite-element%20shallow-water%20models%2C%20with%20application%20to%20the%20Scheldt%20Estuary.%20%26lt%3Bi%26gt%3BAdvances%20in%20Water%20Resources%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B32%26lt%3B%5C%2Fi%26gt%3B%2812%29%2C%201726%26%23x2013%3B1739.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.advwatres.2009.09.005%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.advwatres.2009.09.005%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20flux-limiting%20wetting%5Cu2013drying%20method%20for%20finite-element%20shallow-water%20models%2C%20with%20application%20to%20the%20Scheldt%20Estuary%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Olivier%22%2C%22lastName%22%3A%22Gourgue%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%22%2C%22lastName%22%3A%22Comblen%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Tuomas%22%2C%22lastName%22%3A%22K%5Cu00e4rn%5Cu00e4%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22We%20present%20a%20flux-limiting%20wetting%5Cu2013drying%20approach%20for%20finite-element%20discretizations%20of%20the%20shallow-water%20equations%20using%20discontinuous%20linear%20elements%20for%20the%20elevation.%20The%20key%20ingredient%20of%20the%20method%20is%20the%20use%20of%20limiters%20for%20generalized%20nodal%20fluxes.%20This%20method%20is%20implemented%20into%20the%20Second-generation%20Louvain-la-Neuve%20Ice-ocean%20Model%20%28SLIM%29%2C%20and%20is%20verified%20against%20standard%20test%20cases.%20The%20method%20is%20further%20applied%20to%20the%20wetting%20and%20drying%20of%20sand%20banks%20in%20the%20Scheldt%20Estuary%2C%20which%20is%20located%20in%20northern%20Belgium%20and%20the%20southern%20Netherlands.%20The%20results%20obtained%20for%20both%20the%20benchmarks%20and%20the%20realistic%20problem%20illustrate%20the%20accuracy%20of%20the%20method%20in%20describing%20the%20hydrodynamics%20in%20the%20vicinity%20of%20dry%20areas.%20In%20particular%2C%20the%20method%20strictly%20conserves%20mass%2C%20and%20there%20is%20no%20transport%20through%20dry%20areas.%22%2C%22date%22%3A%22December%202009%22%2C%22language%22%3A%22%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.advwatres.2009.09.005%22%2C%22ISSN%22%3A%220309-1708%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fwww.sciencedirect.com%5C%2Fscience%5C%2Farticle%5C%2Fpii%5C%2FS0309170809001493%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%2C%227VXM6D4Z%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A52%3A26Z%22%7D%7D%2C%7B%22key%22%3A%22N8MJQQV6%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Lambrechts%20et%20al.%22%2C%22parsedDate%22%3A%222008%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BLambrechts%2C%20J.%2C%20Hanert%2C%20E.%2C%20Deleersnijder%2C%20E.%2C%20Bernard%2C%20P.-E.%2C%20Legat%2C%20V.%2C%20Remacle%2C%20J.-F.%2C%20%26amp%3B%20Wolanski%2C%20E.%20%282008%29.%20A%20multi-scale%20model%20of%20the%20hydrodynamics%20of%20the%20whole%20Great%20Barrier%20Reef.%20%26lt%3Bi%26gt%3BEstuarine%2C%20Coastal%20and%20Shelf%20Science%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B79%26lt%3B%5C%2Fi%26gt%3B%281%29%2C%20143%26%23x2013%3B151.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecss.2008.03.016%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecss.2008.03.016%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20multi-scale%20model%20of%20the%20hydrodynamics%20of%20the%20whole%20Great%20Barrier%20Reef%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Paul-Emile%22%2C%22lastName%22%3A%22Bernard%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jean-Fran%5Cu00e7ois%22%2C%22lastName%22%3A%22Remacle%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Wolanski%22%7D%5D%2C%22abstractNote%22%3A%22An%20unstructured-mesh%20parallel%20hydrodynamic%20model%20of%20the%20whole%20Great%20Barrier%20Reef%20is%20presented.%20This%20model%20simultaneously%20simulates%20most%20scales%20of%20motion.%20It%20allows%20interactions%20between%20small-%20and%20largescale%20processes.%20The%20depth-averaged%20equations%20of%20motion%20are%20discretized%20in%20space%20by%20means%20of%20a%20mixed%20%5Cufb01nite%20element%20formulation%20while%20the%20time-marching%20procedure%20is%20based%20on%20a%20third%20order%20explicit%20Adams%5Cu2013Bashforth%20scheme.%20The%20mesh%20is%20made%20up%20of%20triangles.%20Their%20size%20and%20shape%20can%20be%20modi%5Cufb01ed%20easily%20so%20as%20to%20resolve%20a%20wide%20range%20of%20scales%20of%20motion%2C%20from%20those%20of%20the%20regional%20%5Cufb02ows%20to%20those%20of%20the%20eddies%20or%20tidal%20jets%20that%20develop%20in%20the%20vicinity%20of%20reefs%20and%20islands.%20The%20forcings%20are%20the%20surface%20wind%20stress%2C%20the%20tides%20and%20the%20in%5Cufb02ow%20from%20the%20Coral%20Sea%20%28East%20Australian%20Current%2C%20Coral%20Sea%20Coastal%20Current%29%2C%20the%20latter%20two%20forcings%20being%20applied%20along%20the%20open%20boundaries%20of%20the%20computational%20domain.%20The%20numerical%20results%20compare%20favourably%20with%20observations%20of%20both%20longshore%20currents%20and%20the%20local%20perturbations%20due%20to%20narrow%20reef%20passages.%20Comparisons%20are%20also%20performed%20with%20the%20simulations%20of%20a%20three-dimensional%20model%20applied%20to%20a%20small%20domain%20centered%20on%20Rattray%20Island%2C%20showing%20that%20both%20models%20produce%20similar%20horizontal%20%5Cufb02ow%20%5Cufb01elds.%20For%20a%20structured-mesh%20model%20to%20yield%20results%20of%20the%20same%20accuracy%2C%20there%20is%20no%20doubt%20that%20the%20computational%20cost%20would%20be%20much%20higher.%22%2C%22date%22%3A%228%5C%2F2008%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ecss.2008.03.016%22%2C%22ISSN%22%3A%2202727714%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0272771408001364%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A54%3A36Z%22%7D%7D%2C%7B%22key%22%3A%22CCHYX6XR%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Hanert%20et%20al.%22%2C%22parsedDate%22%3A%222005%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%26lt%3Bdiv%20class%3D%26quot%3Bcsl-bib-body%26quot%3B%20style%3D%26quot%3Bline-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%26quot%3B%26gt%3B%5Cn%20%20%26lt%3Bdiv%20class%3D%26quot%3Bcsl-entry%26quot%3B%26gt%3BHanert%2C%20E.%2C%20Roux%2C%20D.%20Y.%20L.%2C%20Legat%2C%20V.%2C%20%26amp%3B%20Deleersnijder%2C%20E.%20%282005%29.%20An%20efficient%20Eulerian%20finite%20element%20method%20for%20the%20shallow%20water%20equations.%20%26lt%3Bi%26gt%3BOcean%20Modelling%26lt%3B%5C%2Fi%26gt%3B%2C%20%26lt%3Bi%26gt%3B10%26lt%3B%5C%2Fi%26gt%3B%281%26%23x2013%3B2%29%2C%20115%26%23x2013%3B136.%20%26lt%3Ba%20class%3D%26%23039%3Bzp-DOIURL%26%23039%3B%20href%3D%26%23039%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2004.06.006%26%23039%3B%26gt%3Bhttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2004.06.006%26lt%3B%5C%2Fa%26gt%3B%26lt%3B%5C%2Fdiv%26gt%3B%5Cn%26lt%3B%5C%2Fdiv%26gt%3B%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22An%20efficient%20Eulerian%20finite%20element%20method%20for%20the%20shallow%20water%20equations%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Daniel%20Y.%20Le%22%2C%22lastName%22%3A%22Roux%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22The%20accuracy%20and%20e%5Cufb03ciency%20of%20an%20Eulerian%20method%20is%20assessed%20by%20solving%20the%20non-linear%20shallow%20water%20equations%20and%20compared%20with%20the%20performances%20of%20an%20existing%20semi-Lagrangian%20method.%20Both%20methods%20use%20a%20linear%20non-conforming%20%5Cufb01nite%20element%20discretization%20for%20velocity%20and%20a%20linear%20conforming%20%5Cufb01nite%20element%20discretization%20for%20surface%20elevation.%20This%20%5Cufb01nite%20element%20pair%20is%20known%20to%20be%20computationally%20e%5Cufb03cient%20and%20free%20of%20pressure%20modes.%20The%20model%20equations%20are%20carefully%20derived%20and%20a%20comparison%20is%20performed%20by%20simulating%20the%20propagation%20of%20slow%20Rossby%20waves%20in%20the%20Gulf%20of%20Mexico.%20Simulations%20show%20that%20the%20Eulerian%20model%20performs%20well%20and%20gives%20results%20comparable%20to%20high%20order%20semi-Lagrangian%20schemes%20using%20kriging%20interpolators.%22%2C%22date%22%3A%221%5C%2F2005%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ocemod.2004.06.006%22%2C%22ISSN%22%3A%2214635003%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS1463500304000678%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T11%3A13%3A07Z%22%7D%7D%5D%7D
Scherpereel, C., Alosairi, Y., Lambrechts, J., & Hanert, E. (2025). Hydrodynamic impacts of bridge construction and land reclamation on water residence time and flushing processes in Kuwait Bay.
Marine Pollution Bulletin ,
214 , 117716.
https://doi.org/10.1016/j.marpolbul.2025.117716
Hirsh, H. K., Oliver, T. A., Dobbelaere, T., Palacio-Castro, A. M., Barkley, H. C., Webb, A. E., Hanert, E., & Enochs, I. C. (2025). Statistical Prediction of In Situ Coral Reef Carbonate Dynamics Using Endmember Chemistry, Hydrodynamic Models, And Benthic Composition.
Aquatic Geochemistry ,
31 (1), 4.
https://doi.org/10.1007/s10498-025-09438-x
Dobbelaere, T., Holstein, D. M., Gramer, L. J., McEachron, L., & Hanert, E. (2024). Investigating the link between the Port of Miami dredging and the onset of the stony coral tissue loss disease epidemics.
Marine Pollution Bulletin ,
207 , 116886.
https://doi.org/10.1016/j.marpolbul.2024.116886
Dobbelaere, T., Dekens, A., Saint‐Amand, A., Alaerts, L., Holstein, D. M., & Hanert, E. (2024). Hurricanes enhance coral connectivity but also superspread coral diseases.
Global Change Biology ,
30 (6), e17382.
https://doi.org/10.1111/gcb.17382
Faryuni, I. D., Saint-Amand, A., Dobbelaere, T., Umar, W., Jompa, J., Moore, A. M., & Hanert, E. (2024). Assessing coral reef conservation planning in Wakatobi National Park (Indonesia) from larval connectivity networks.
Coral Reefs ,
43 (1), 19–33.
https://doi.org/10.1007/s00338-023-02443-y
Lecart, M., Dobbelaere, T., Alaerts, L., Randresihaja, N. R., Mohammed, A. V., Vethamony, P., & Hanert, E. (2024). Land reclamation and its consequences: A 40-year analysis of water residence time in Doha Bay, Qatar.
PLOS ONE ,
19 (1), e0296715.
https://doi.org/10.1371/journal.pone.0296715
Saint-Amand, A., Lambrechts, J., & Hanert, E. (2023). Biophysical models resolution affects coral connectivity estimates.
Scientific Reports ,
13 (1), 9414.
https://doi.org/10.1038/s41598-023-36158-5
Purkis, S. J., Oehlert, A. M., Dobbelaere, T., Hanert, E., & Harris, P. (Mitch). (2023). Always a White Christmas in the Bahamas: temperature and hydrodynamics localize winter mud production on Great Bahama Bank.
Journal of Sedimentary Research ,
93 (3), 145–160.
https://doi.org/10.2110/jsr.2022.066
King, S., Saint-Amand, A., Walker, B. K., Hanert, E., & Figueiredo, J. (2023). Larval dispersal patterns and connectivity of Acropora on Florida’s Coral Reef and its implications for restoration.
Frontiers in Marine Science ,
9 , 1038463.
https://doi.org/10.3389/fmars.2022.1038463
Sampurno, J., Ardianto, R., & Hanert, E. (2023). Integrated machine learning and GIS-based bathtub models to assess the future flood risk in the Kapuas River Delta, Indonesia.
Journal of Hydroinformatics ,
25 (1), 113–125.
https://doi.org/10.2166/hydro.2022.106
Saint-Amand, A., Lambrechts, J., Thomas, C. J., & Hanert, E. (2023). How fine is fine enough? Effect of mesh resolution on hydrodynamic simulations in coral reef environments.
Ocean Modelling ,
186 , 102254.
https://doi.org/10.1016/j.ocemod.2023.102254
Verhofstede, A., Dobbelaere, T., Harlay, J., & Hanert, E. (2023). Seychelles Plateau’s oil spill vulnerability.
Marine Pollution Bulletin ,
196 , 115652.
https://doi.org/10.1016/j.marpolbul.2023.115652
Patterson, R. G., Wolanski, E., Groom, R., Critchell, K., Playford, L., Grubert, M., Kennett, R., Tait, H., Udyawer, V., Lambrechts, J., & Campbell, H. A. (2023). Improving certainty in marine ecosystems: A biophysical modelling approach in the remote, data-limited Gulf of Carpentaria.
Estuarine, Coastal and Shelf Science ,
283 , 108254.
https://doi.org/10.1016/j.ecss.2023.108254
Hanert, E., Mohammed, A. V., Veerasingam, S., Dobbelaere, T., Vallaeys, V., & Vethamony, P. (2023). A multiscale ocean modelling system for the central Arabian/Persian Gulf: From regional to structure scale circulation patterns.
Estuarine, Coastal and Shelf Science ,
282 , 108230.
https://doi.org/10.1016/j.ecss.2023.108230
Sampurno, J., Vallaeys, V., Ardianto, R., & Hanert, E. (2022). Integrated hydrodynamic and machine learning models for compound flooding prediction in a data-scarce estuarine delta.
Nonlinear Processes in Geophysics ,
29 (3), 301–315.
https://doi.org/10.5194/npg-29-301-2022
Sampurno, J., Vallaeys, V., Ardianto, R., & Hanert, E. (2022). Modeling interactions between tides, storm surges, and river discharges in the Kapuas River delta.
Biogeosciences ,
19 (10), 2741–2757.
https://doi.org/10.5194/bg-19-2741-2022
Sampurno, J., Vallaeys, V., Ardianto, R., & Hanert, E. (2022). Modeling interactions between tides, storm surges, and river discharges in the Kapuas River delta.
Biogeosciences ,
19 (10), 2741–2757.
https://doi.org/10.5194/bg-19-2741-2022
Saint-Amand, A., Grech, A., Choukroun, S., & Hanert, E. (2022). Quantifying the environmental impact of a major coal mine project on the adjacent Great Barrier Reef ecosystems.
Marine Pollution Bulletin ,
179 , 113556.
https://doi.org/j.marpolbul.2022.113656
Dobbelaere, T., Holstein, D. M., Muller, E. M., Gramer, L. J., McEachron, L., Williams, S. D., & Hanert, E. (2022). Connecting the Dots: Transmission of Stony Coral Tissue Loss Disease From the Marquesas to the Dry Tortugas.
Frontiers in Marine Science ,
9 , 778938.
https://doi.org/10.3389/fmars.2022.778938
Vincent, D., Lambrechts, J., Tyler, R. H., Karatekin, Ö., Dehant, V., & Deleersnijder, É. (2022). A numerical study of the liquid motion in Titan’s subsurface ocean.
Icarus ,
388 , 115219.
https://doi.org/10.1016/j.icarus.2022.115219
Lopez‐Gamundi, C., Dobbelaere, T., Hanert, E., Harris, P. M., Eberli, G., & Purkis, S. J. (2022). Simulating sedimentation on the Great Bahama Bank – Sources, sinks and storms.
Sedimentology ,
69 (7), 2693–2714.
https://doi.org/10.1111/sed.13020
Dobbelaere, T., Curcic, M., Le Hénaff, M., & Hanert, E. (2022). Impacts of Hurricane Irma (2017) on wave-induced ocean transport processes.
Ocean Modelling ,
171 , 101947.
https://doi.org/10.1016/j.ocemod.2022.101947
Wolanski, E., & Hopper, C. (2022). Dams and climate change accelerate channel avulsion and coastal erosion and threaten Ramsar-listed wetlands in the largest Great Barrier Reef watershed.
Ecohydrology & Hydrobiology , S1642359322000015.
https://doi.org/10.1016/j.ecohyd.2022.01.001
Figueiredo, J., Thomas, C. J., Deleersnijder, E., Lambrechts, J., Baird, A. H., Connolly, S. R., & Hanert, E. (2022). Global warming decreases connectivity among coral populations.
Nature Climate Change ,
12 (1), 83–87.
https://doi.org/10.1038/s41558-021-01248-7
Le, H.-A., Lambrechts, J., Deleersnijder, E., Soares-Frazao, S., Gratiot, N., Ortleb, S., & Deleersnijder, E. (2020). Numerical modelling of flow dynamics in the Tonle Sap by means of a discontinuous Galerkin finite-element model. In W. Uijttewaal, M. J. Franca, D. Valero, V. Chavarrias, C. Ylla Arbós, R. Schielen, & A. Crosato (Eds.), River Flow 2020 (1st ed., pp. 1148–1154). CRC Press. https://doi.org/10.1201/b22619-160
Frys, C., Saint-Amand, A., Le Hénaff, M., Figueiredo, J., Kuba, A., Walker, B., Lambrechts, J., Vallaeys, V., Vincent, D., & Hanert, E. (2020). Fine-Scale Coral Connectivity Pathways in the Florida Reef Tract: Implications for Conservation and Restoration.
Frontiers in Marine Science ,
7 .
https://doi.org/10.3389/fmars.2020.00312
Le, H.-A., Lambrechts, J., Ortleb, S., Gratiot, N., Deleersnijder, E., & Soares-Frazão, S. (2020). An implicit wetting–drying algorithm for the discontinuous Galerkin method: application to the Tonle Sap, Mekong River Basin.
Environmental Fluid Mechanics .
https://doi.org/10.1007/s10652-019-09732-7
Le, H.-A., Gratiot, N., Santini, W., Ribolzi, O., Tran, D., Meriaux, X., Deleersnijder, E., & Soares-Frazão, S. (2020). Suspended sediment properties in the Lower Mekong River, from fluvial to estuarine environments.
Estuarine, Coastal and Shelf Science ,
233 , 106522.
https://doi.org/10.1016/j.ecss.2019.106522
Dobbelaere, T., Muller, Erinn, Gramer, Lewis, Holstein, Daniel, & Hanert, E. (2020). Coupled Epidemio-Hydrodynamic Modeling to Understand the Spread of a Deadly Coral Disease in Florida.
Frontiers in Marine Science ,
7 , 16.
https://doi.org/10.3389/fmars.2020.591881
Vincent, D., Lambrechts, J., Karatekin, Ö., Van Hoolst, T., Tyler, R. H., Dehant, V., & Deleersnijder, E. (2019). Normal modes and resonance in Ontario Lacus: a hydrocarbon lake of Titan.
Ocean Dynamics .
https://doi.org/10.1007/s10236-019-01290-2
Vincent, D., Karatekin, Ö., Lambrechts, J., Lorenz, R. D., Dehant, V., & Deleersnijder, É. (2018). A numerical study of tides in Titan′s northern seas, Kraken and Ligeia Maria.
Icarus ,
310 , 105–126.
https://doi.org/10.1016/j.icarus.2017.12.018
Delandmeter, P., Lambrechts, J., Marmorino, G. O., Legat, V., Wolanski, E., Remacle, J.-F., Chen, W., & Deleersnijder, E. (2017). Submesoscale tidal eddies in the wake of coral islands and reefs: satellite data and numerical modelling.
Ocean Dynamics ,
67 (7), 897–913.
https://doi.org/10.1007/s10236-017-1066-z
Pham Van, C., de Brye, B., Deleersnijder, E., Hoitink, A. J. F., Sassi, M., Spinewine, B., Hidayat, H., & Soares-Frazão, S. (2016). Simulations of the flow in the Mahakam river–lake–delta system, Indonesia.
Environmental Fluid Mechanics ,
16 (3), 603–633.
https://doi.org/10.1007/s10652-016-9445-4
Vincent, D., Karatekin, Ö., Vallaeys, V., Hayes, A. G., Mastrogiuseppe, M., Notarnicola, C., Dehant, V., & Deleersnijder, E. (2016). Numerical study of tides in Ontario Lacus, a hydrocarbon lake on the surface of the Saturnian moon Titan.
Ocean Dynamics ,
66 (4), 461–482.
https://doi.org/10.1007/s10236-016-0926-2
Le Bars, Y., Vallaeys, V., Deleersnijder, É., Hanert, E., Carrere, L., & Channelière, C. (2016). Unstructured-mesh modeling of the Congo river-to-sea continuum.
Ocean Dynamics ,
66 (4), 589–603.
https://doi.org/10.1007/s10236-016-0939-x
Thomas, C. J., Lambrechts, J., Wolanski, E., Traag, V. A., Blondel, V. D., Deleersnijder, E., & Hanert, E. (2014). Numerical modelling and graph theory tools to study ecological connectivity in the Great Barrier Reef.
Ecological Modelling ,
272 , 160–174.
https://doi.org/10.1016/j.ecolmodel.2013.10.002
Kärnä, T., de Brye, B., Gourgue, O., Lambrechts, J., Comblen, R., Legat, V., & Deleersnijder, E. (2011). A fully implicit wetting–drying method for DG-FEM shallow water models, with an application to the Scheldt Estuary.
Computer Methods in Applied Mechanics and Engineering ,
200 (5–8), 509–524.
https://doi.org/10.1016/j.cma.2010.07.001
de Brye, B., Schellen, S., Sassi, M., Vermeulen, B., Kärnä, T., Deleersnijder, E., & Hoitink, T. (2011). Preliminary results of a finite-element, multi-scale model of the Mahakam Delta (Indonesia).
Ocean Dynamics ,
61 (8), 1107–1120.
https://doi.org/10.1007/s10236-011-0410-y
de Brye, B., de Brauwere, A., Gourgue, O., Kärnä, T., Lambrechts, J., Comblen, R., & Deleersnijder, E. (2010). A finite-element, multi-scale model of the Scheldt tributaries, river, estuary and ROFI.
Coastal Engineering ,
57 (9), 850–863.
https://doi.org/10.1016/j.coastaleng.2010.04.001
Gourgue, O., Comblen, R., Lambrechts, J., Kärnä, T., Legat, V., & Deleersnijder, E. (2009). A flux-limiting wetting–drying method for finite-element shallow-water models, with application to the Scheldt Estuary.
Advances in Water Resources ,
32 (12), 1726–1739.
https://doi.org/10.1016/j.advwatres.2009.09.005
Lambrechts, J., Hanert, E., Deleersnijder, E., Bernard, P.-E., Legat, V., Remacle, J.-F., & Wolanski, E. (2008). A multi-scale model of the hydrodynamics of the whole Great Barrier Reef.
Estuarine, Coastal and Shelf Science ,
79 (1), 143–151.
https://doi.org/10.1016/j.ecss.2008.03.016
Hanert, E., Roux, D. Y. L., Legat, V., & Deleersnijder, E. (2005). An efficient Eulerian finite element method for the shallow water equations.
Ocean Modelling ,
10 (1–2), 115–136.
https://doi.org/10.1016/j.ocemod.2004.06.006