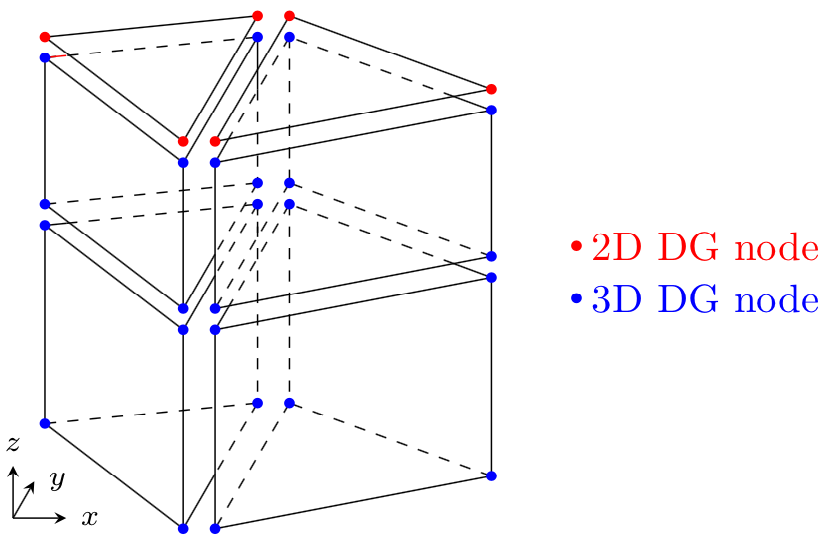
SLIM3D solves the three-dimensional hydrostatic equations under the Boussinesq approximation. The model variables are the 3D velocity, the surface elevation, the salinity and the temperature. The density is obtained by means of an equation of state. SLIM3D uses a mesh composed of triangular prismatic elements that are formed by extruding the 2D unstructured mesh in the vertical direction. The model equations are solved by means of the Discontinuous Galerkin finite element method.
Sketch of the 3D mesh obtained by vertically extruding a 2D triangular mesh. All variables are piecewise linear and discontinuous between elements. One key aspect in any 3D ocean model is the coupling between the external and internal modes. SLIM3D uses a mode-splitting formulation in which the fast propagating gravity waves are solved in an external 2D mode. That mode can either be discretised explicitly with a small time step or implicitly with a larger time step.
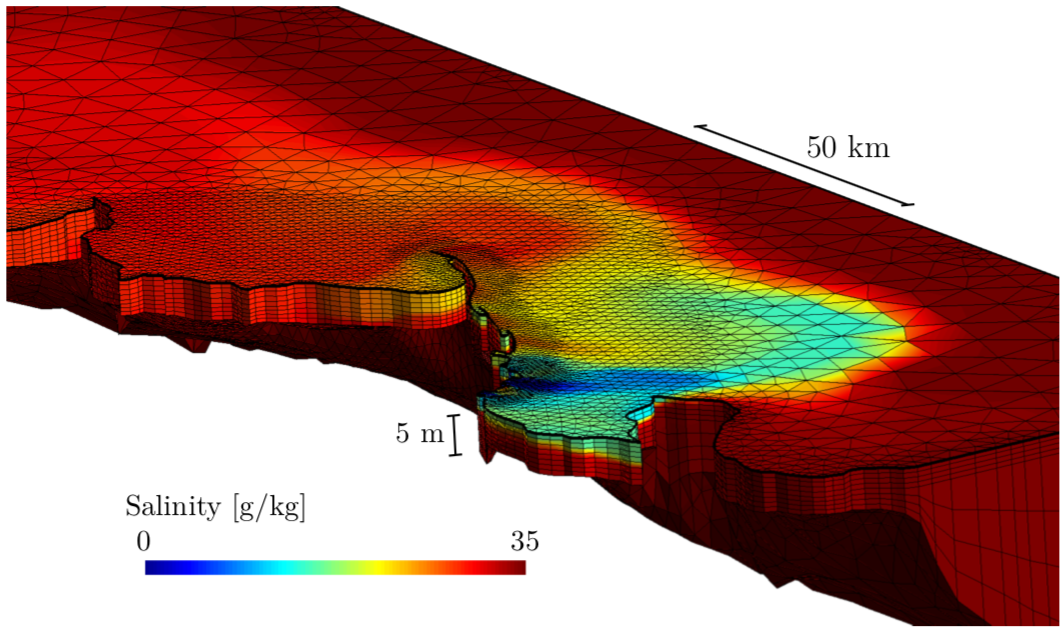
3D mesh used to simulate the sediment plume dynamics of the Burdekine River (Australia). The bathymetry being quite shallow and smooth, sigma layers are sufficient to provide an accurate solution. In the vertical, SLIM3D allows a combination of z and sigma layers. For rather shallow environments with mild bathymetry gradients, sigma coordinates can be used over the entire water column. For deeper areas with sharp bathymetry gradients, sigma layers are generally used only near the surface while z layers are used in the rest of the domain. The number of z layers can be adapted to better approximate bathymetry gradients.
The accuracy of the mode coupling has been tested on a baroclinic test case described in Ilicak et al. (2012). The domain is a periodic (along the 500km-long boundaries) and closed (along the 160km-long boundaries) channel with a bathymetry of 1000m (exaggerated on the video). The large bottom drag coefficient and asymmetric initial condition trigger baroclinic instabilities in the channel. The 4km mesh resolution is similar to one of typical mesoscale eddy permitting models. SLIM3D is able to reproduce the development of baroclinic eddies, as illustrated by the evolution of the predicted temperature.
To learn more…
778265
SLIM3D
items
1
0
date
desc
6983
https://www.slim-ocean.be/wp-content/plugins/zotpress/
%7B%22status%22%3A%22success%22%2C%22updateneeded%22%3Afalse%2C%22instance%22%3A%22zotpress-ff13be4f0362cdc02bf98df886e2c146%22%2C%22meta%22%3A%7B%22request_last%22%3A0%2C%22request_next%22%3A0%2C%22used_cache%22%3Atrue%7D%2C%22data%22%3A%5B%7B%22key%22%3A%22X9QH2ZB6%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Sterckx%20et%20al.%22%2C%22parsedDate%22%3A%222023-01-10%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESterckx%2C%20K.%2C%20Delandmeter%2C%20P.%2C%20Lambrechts%2C%20J.%2C%20Deleersnijder%2C%20E.%2C%20Verburg%2C%20P.%2C%20%26amp%3B%20Thiery%2C%20W.%20%282023%29.%20The%20impact%20of%20seasonal%20variability%20and%20climate%20change%20on%20lake%20Tanganyika%26%23x2019%3Bs%20hydrodynamics.%20%3Ci%3EEnvironmental%20Fluid%20Mechanics%3C%5C%2Fi%3E.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10652-022-09908-8%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10652-022-09908-8%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22The%20impact%20of%20seasonal%20variability%20and%20climate%20change%20on%20lake%20Tanganyika%5Cu2019s%20hydrodynamics%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Kevin%22%2C%22lastName%22%3A%22Sterckx%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Philippe%22%2C%22lastName%22%3A%22Delandmeter%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Piet%22%2C%22lastName%22%3A%22Verburg%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Wim%22%2C%22lastName%22%3A%22Thiery%22%7D%5D%2C%22abstractNote%22%3A%22In%20this%20paper%2C%20we%20project%20future%20changes%20in%20the%20hydrodynamics%20of%20Lake%20Tanganyika%20under%20a%20high%20emission%20scenario%20using%20the%20three-dimensional%20%283D%29%20version%20of%20the%20Second-generation%20Louvain-la-Neuve%20Ice-ocean%20Model%20%28SLIM%203D%29%20forced%20by%20a%20high-resolution%20regional%20climate%20model.%20We%20demonstrate%20the%20advantages%20of%203D%20simulation%20compared%20to%201D%20vertical%20models.%20The%20model%20captures%20the%20seasonal%20variability%20in%20the%20lake%2C%20with%20seasonal%20deep%20mixing%20and%20surfacing%20of%20the%20thermocline.%20In%20a%20simulation%20of%20current%20conditions%2C%20the%20thermocline%20in%20the%20south%20of%20the%20lake%20moves%20upward%20from%20a%20depth%20of%2075%20m%20until%20it%20reaches%20the%20lake%20surface%20during%20August%20and%20September.%20We%20compare%20the%20current%20conditions%20with%20an%20end-of-the-century%20simulation%20under%20a%20pessimistic%20emission%20scenario%20%28RCP%208.5%29%20showing%20that%20surface%20water%20temperature%20increases%20on%20average%20by%203%5Cu2009%5Cu00b1%5Cu20090.5%20%5Cu00b0C.%20Because%20deeper%20water%20warms%20less%2C%20the%20stratification%20increases%20in%20the%20upper%20150%20m%20of%20the%20water%20column.%20This%20temperature-induced%20stratification%20reduces%20mixing%20and%20prevents%20the%20outcropping%20of%20the%20thermocline%2C%20eventually%20shutting%20down%20the%20ventilation%20of%20deep%20water%20in%20the%20south%20basin.%20Our%20results%20highlight%20the%20extreme%20changes%20likely%20faced%20by%20Lake%20Tanganyika%20if%20global%20greenhouse%20gas%20emissions%20are%20not%20curbed.%22%2C%22date%22%3A%222023-01-10%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs10652-022-09908-8%22%2C%22ISSN%22%3A%221567-7419%2C%201573-1510%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs10652-022-09908-8%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-03-05T15%3A27%3A10Z%22%7D%7D%2C%7B%22key%22%3A%22TWXQ965G%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Ishimwe%20et%20al.%22%2C%22parsedDate%22%3A%222023%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EIshimwe%2C%20A.%20P.%2C%20Deleersnijder%2C%20E.%2C%20Legat%2C%20V.%2C%20%26amp%3B%20Lambrechts%2C%20J.%20%282023%29.%20A%20split-explicit%20second%20order%20Runge%26%23x2013%3BKutta%20method%20for%20solving%203D%20hydrodynamic%20equations.%20%3Ci%3EOcean%20Modelling%3C%5C%2Fi%3E%2C%20%3Ci%3E186%3C%5C%2Fi%3E%2C%20102273.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2023.102273%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2023.102273%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20split-explicit%20second%20order%20Runge%5Cu2013Kutta%20method%20for%20solving%203D%20hydrodynamic%20equations%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ange%20Pacifique%22%2C%22lastName%22%3A%22Ishimwe%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%5D%2C%22abstractNote%22%3A%22Numerical%20models%20of%20marine%20hydrodynamics%20have%20to%20deal%20with%20processes%20exhibiting%20a%20wide%20range%20of%20timescales.%20These%20processes%20include%20fast%20external%20gravity%20waves%20and%20slower%20internal%20fully%20three-dimensional%20motions.%20In%20order%20to%20be%20both%20time-efficient%20and%20numerically%20stable%2C%20the%20time%20stepping%20scheme%20has%20to%20be%20chosen%20carefully%20to%20cope%20with%20the%20characteristic%20time%20scale%20of%20each%20phenomenon.%20An%20usual%20approach%20is%20to%20split%20the%20fast%20and%20slow%20dynamics%20into%20separate%20modes.%20The%20fast%20waves%20are%20modeled%20with%20a%20two-dimensional%20system%20through%20depth%20averaging%20while%20the%20other%20motions%2C%20where%20characteristic%20times%20are%20much%20longer%2C%20are%20dealt%20with%20in%20three%20dimensions.%20However%2C%20if%20the%20splitting%20is%20inexact%2C%20for%20instance%20in%20projecting%20the%20fields%20in%20a%20new%203D%20mesh%2C%20this%20procedure%20can%20lead%20to%20improper%20results%20regarding%20to%20the%20physical%20properties%20such%20as%20mass%20conservation%20and%20tracer%20consistency.%20In%20this%20work%2C%20a%20new%20split-explicit%20Runge%5Cu2013Kutta%20scheme%20is%20adapted%20and%20developed%20for%20the%20Discontinuous-Galerkin%20Finite%20Element%20method%20in%20order%20to%20obtain%20a%20new%20second-order%20time%20stepping%2C%20yielding%20to%20more%20accurate%20results.%20This%20method%20combines%20a%20three-stage%20low-storage%20Runge%5Cu2013Kutta%20for%20the%20slow%20processes%20and%20a%20two-stage%20low-storage%20for%20the%20fast%20ones.%20The%203D%20iterations%20are%20not%20affecting%20the%20surface%20elevation%2C%20hence%20an%20Arbitrary%20Lagrangian%20Eulerian%20implementation%20is%20straightforward.%20Water%20volume%20and%20tracers%20are%20conserved.%20A%20set%20of%20test%20cases%20for%20baroclinic%20flows%20as%20well%20as%20a%20laboratory%20application%20demonstrate%20the%20performance%20of%20the%20scheme.%20They%20suggest%20that%20the%20new%20scheme%20has%20little%20numerical%20diffusion.%22%2C%22date%22%3A%2212%5C%2F2023%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ocemod.2023.102273%22%2C%22ISSN%22%3A%2214635003%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS1463500323001130%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222023-09-21T08%3A37%3A17Z%22%7D%7D%2C%7B%22key%22%3A%22WZB32C98%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Alaerts%20et%20al.%22%2C%22parsedDate%22%3A%222022-07-11%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EAlaerts%2C%20L.%2C%20Dobbelaere%2C%20T.%2C%20Gravinese%2C%20P.%20M.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282022%29.%20Climate%20Change%20Will%20Fragment%20Florida%20Stone%20Crab%20Communities.%20%3Ci%3EFrontiers%20in%20Marine%20Science%3C%5C%2Fi%3E%2C%20%3Ci%3E9%3C%5C%2Fi%3E%2C%20839767.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.3389%5C%2Ffmars.2022.839767%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.3389%5C%2Ffmars.2022.839767%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Climate%20Change%20Will%20Fragment%20Florida%20Stone%20Crab%20Communities%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Lauranne%22%2C%22lastName%22%3A%22Alaerts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Thomas%22%2C%22lastName%22%3A%22Dobbelaere%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Philip%20M.%22%2C%22lastName%22%3A%22Gravinese%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22Many%20marine%20species%20have%20been%20shown%20to%20be%20threatened%20by%20both%20ocean%20acidi%5Cufb01cation%20and%20ocean%20warming%20which%20are%20reducing%20survival%2C%20altering%20behavior%2C%20and%20posing%20limits%20on%20physiology%2C%20especially%20during%20earlier%20life%20stages.%20The%20commercially%20important%20Florida%20stone%20crab%2C%20Menippe%20mercenaria%2C%20is%20one%20species%20that%20is%20affected%20by%20reduced%20seawater%20pH%20and%20elevated%20seawater%20temperatures.%20In%20this%20study%2C%20we%20determined%20the%20impacts%20of%20reduced%20pH%20and%20elevated%20temperature%20on%20the%20distribution%20of%20the%20stone%20crab%20larvae%20along%20the%20West%20Florida%20Shelf.%20To%20understand%20the%20dispersion%20of%20the%20larvae%2C%20we%20coupled%20the%20multiscale%20ocean%20model%20SLIM%20with%20a%20larval%20dispersal%20model.%20We%20then%20conducted%20a%20connectivity%20study%20and%20evaluated%20the%20impacts%20of%20climate%20stressors%20by%20looking%20at%20four%20different%20scenarios%20which%20included%20models%20that%20represented%20the%20dispersion%20of%20stone%20crab%20larvae%20under%3A%201%29%20present%20day%20conditions%20as%20modelled%20by%20SLIM%20for%20the%20temperature%20and%20NEMO-PISCES%20for%20the%20pH%2C%202%29%20SSP1-2.6%20scenario%20%28-0.037%20reduction%20in%20pH%20and%20%2B0.5%5Cu00b0C%20compared%20to%20presentday%20conditions%29%2C%203%29%20SSP2-4.5%20scenario%28-0.15%20reduction%20in%20pH%20and%20%2B1.5%5Cu00b0C%29%20and%204%29%20SSP5-8.5%20scenario%20%28-0.375%20reduction%20in%20pH%20and%20%2B3.5%5Cu00b0C%29.%20Our%20results%20show%20a%20clear%20impact%20of%20these%20climate%20change%20stressors%20on%20larval%20dispersal%20and%20on%20the%20subsequent%20stone%20crab%20distribution.%20Our%20results%20indicate%20that%20future%20climate%20change%20could%20result%20in%20stone%20crabs%20moving%20north%20or%20into%20deeper%20waters.%20We%20also%20observed%20an%20increase%20in%20the%20number%20of%20larvae%20settling%20in%20deeper%20waters%20%28de%5Cufb01ned%20as%20the%20non-%5Cufb01shing%20zone%20in%20this%20study%20with%20depths%20exceeding%2030%20m%29%20that%20are%20not%20typically%20part%20of%20the%20commercial%20%5Cufb01shing%20zone.%20The%20distance%20travelled%20by%20larvae%2C%20however%2C%20is%20likely%20to%20decrease%2C%20resulting%20in%20an%20increase%20of%20selfrecruitment%20and%20decrease%20of%20the%20size%20of%20the%20sub-populations.%20A%20shift%20of%20the%20spawning%20period%2C%20to%20earlier%20in%20the%20spring%2C%20is%20also%20likely%20to%20occur.%20Our%20results%20suggest%20that%20habitats%20in%20the%20non-%5Cufb01shing%20zone%20cannot%20serve%20as%20a%20signi%5Cufb01cant%20source%20of%20larvae%20for%20the%20habitats%20in%20the%20%5Cufb01shing%20zone%20%28de%5Cufb01ned%20as%20water%20depth%3C%2030%20m%29%20since%20there%20is%20very%20little%20exchange%20%28%3C%205%25%20of%20all%20exchanges%29%20between%20the%20two%20zones.%20These%20results%20indicate%20that%20the%20stone%20crab%20populations%20in%20Florida%20may%20be%20susceptible%20to%20community%20fragmentation%20and%20that%20the%20management%20of%20the%20%5Cufb01shery%20should%20consider%20the%20potential%20impacts%20of%20future%20climate%20change%20scenarios.%22%2C%22date%22%3A%222022-7-11%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.3389%5C%2Ffmars.2022.839767%22%2C%22ISSN%22%3A%222296-7745%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.frontiersin.org%5C%2Farticles%5C%2F10.3389%5C%2Ffmars.2022.839767%5C%2Ffull%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222022-07-11T07%3A13%3A59Z%22%7D%7D%2C%7B%22key%22%3A%22NH4E9UBK%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Vallaeys%20et%20al.%22%2C%22parsedDate%22%3A%222021%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EVallaeys%2C%20V.%2C%20Lambrechts%2C%20J.%2C%20Delandmeter%2C%20P.%2C%20P%26%23xE4%3Btsch%2C%20J.%2C%20Spitzy%2C%20A.%2C%20Hanert%2C%20E.%2C%20%26amp%3B%20Deleersnijder%2C%20E.%20%282021%29.%20Understanding%20the%20circulation%20in%20the%20deep%2C%20micro-tidal%20and%20strongly%20stratified%20Congo%20River%20estuary.%20%3Ci%3EOcean%20Modelling%3C%5C%2Fi%3E%2C%20101890.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2021.101890%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2021.101890%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Understanding%20the%20circulation%20in%20the%20deep%2C%20micro-tidal%20and%20strongly%20stratified%20Congo%20River%20estuary%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Valentin%22%2C%22lastName%22%3A%22Vallaeys%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Philippe%22%2C%22lastName%22%3A%22Delandmeter%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Johannes%22%2C%22lastName%22%3A%22P%5Cu00e4tsch%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Alejandro%22%2C%22lastName%22%3A%22Spitzy%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22The%20Congo%20River%20estuary%20is%20characterised%20by%20a%20deep%20canyon%20that%20connects%20the%20river%20to%20the%20deep%20ocean%20by%20cutting%20through%20the%20continental%20shelf.%20Its%20estuary%20is%20influenced%20by%20high%20river%20discharge%20and%20micro-tidal%20conditions%2C%20with%20a%20large%20depth%20and%20limited%20vertical%20mixing.%20This%20restricts%20the%20supply%20of%20oxygen%20from%20the%20surface%20waters%20to%20the%20more%20saline%20bottom%20waters%2C%20leading%20to%20hypoxic%20and%20anoxic%20zones.%20We%20study%20the%20dynamics%20of%20the%20Congo%20River%20estuary%20by%20applying%20the%20multi-scale%20baroclinic%20coastal%20ocean%20model%20SLIM%203D%20%28www.slim-ocean.be%29%20to%20this%20topographically%20challenging%20environment.%20By%20allowing%20a%20high%20degree%20of%20flexibility%20in%20the%20representation%20of%20both%20the%20complex%20geometry%20and%20the%20strong%20stratification%2C%20SLIM%203D%20is%20able%20to%20simulate%20riverine%2C%20tidal%20and%20gravitational%20processes%20that%20drive%20the%20estuarine%20circulation.%20Model%20results%20compare%20favourably%20with%20in-situ%20data%20in%20the%20estuary%2C%20suggesting%20that%20the%20exchange%20flow%20is%20correctly%20simulated.%20The%20latter%20is%20characterised%20by%20a%20two-layer%20dynamics.%20The%20combination%20of%20the%20large%20river%20discharge%2C%20the%20strong%20stratification%20and%20the%20large%20depth%20results%20in%20a%20moderate%20freshwater%20Froude%20number%20and%20a%20very%20small%20mixing%20number.%20It%20makes%20the%20Congo%20River%20an%20outlier%20in%20state-of-the-art%20estuarine%20classifications%2C%20closer%20to%20fjords%20than%20salt%20wedge%20estuaries.%20Furthermore%2C%20using%20the%20age%20as%20a%20diagnosis%20sheds%20light%20on%20the%20spatial%20variability%20of%20the%20estuarine%20waters%20ventilation.%20Local%20maximum%20of%20renewing%20water%20age%20located%20just%20below%20the%20pycnocline%20is%20exceeded%20by%20old%20dense%20oceanic%20waters%20which%20stagnate%20at%20the%20bottom%20of%20the%20canyon%20for%20more%20than%20two%20months%20due%20to%20the%20small%20vertical%20mixing.%20It%20helps%20explain%20the%20hypoxic%20and%20anoxic%20conditions%20observed%20at%20the%20bottom%20of%20the%20submarine%20canyon.%22%2C%22date%22%3A%229%5C%2F2021%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ocemod.2021.101890%22%2C%22ISSN%22%3A%2214635003%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS1463500321001438%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222021-09-24T16%3A12%3A02Z%22%7D%7D%2C%7B%22key%22%3A%22PBV3FWIZ%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Duquesne%20et%20al.%22%2C%22parsedDate%22%3A%222021%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EDuquesne%2C%20F.%2C%20Vallaeys%2C%20V.%2C%20Vidaurre%2C%20P.%20J.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282021%29.%20A%20coupled%20ecohydrodynamic%20model%20to%20predict%20algal%20blooms%20in%20Lake%20Titicaca.%20%3Ci%3EEcological%20Modelling%3C%5C%2Fi%3E%2C%20%3Ci%3E440%3C%5C%2Fi%3E%2C%20109418.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecolmodel.2020.109418%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecolmodel.2020.109418%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20coupled%20ecohydrodynamic%20model%20to%20predict%20algal%20blooms%20in%20Lake%20Titicaca%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Fran%5Cu00e7ois%22%2C%22lastName%22%3A%22Duquesne%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Valentin%22%2C%22lastName%22%3A%22Vallaeys%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Prem%20Jai%22%2C%22lastName%22%3A%22Vidaurre%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22Lake%20Titicaca%20is%20home%20to%20a%20unique%20high-altitude%20ecosystem%20that%20is%20suffering%20from%20increasing%20anthropogenic%20pressures.%20It%20experienced%20its%20first%20major%20algal%20bloom%20in%20March%5Cu2013April%202015%20that%20had%20devastating%20consequences%20in%20the%20southern%20shallow%20lake%20basin.%20Such%20events%20are%20expected%20to%20intensify%20in%20the%20future%20and%20call%20for%20a%20more%20active%20and%20quantitative%20management%20of%20the%20lake%20and%20its%20watershed.%20In%20this%20paper%20we%20describe%20a%20coupled%20ecohydrodynamic%20model%20to%20predict%20the%20lake%5Cu2019s%20water%20quality%20and%2C%20more%20particularly%2C%20the%20risk%20of%20harmful%20algal%20blooms.%20We%20have%20coupled%20a%20nitrogen-phytoplankton-zooplankton-detritus%20%28NPZD%29%20ecosystem%20model%20to%20the%20unstructured-mesh%203D%20hydrodynamic%20model%20SLIM.%20Our%20high-resolution%20multi-scale%20model%20explicitly%20represents%20the%20exchanges%20between%20the%20two%20basins%20composing%20the%20lake%2C%20through%20the%20narrow%20Strait%20of%20Tiquina.%20This%20allowed%20us%20to%20study%20the%20biophysical%20processes%20driving%20the%20entire%20lake%20over%20the%20period%20of%20January%202014%20to%20May%202015.%20The%20model%20has%20been%20validated%20against%20temperature%20profiles%20at%20several%20locations%20throughout%20the%20lake.%20It%20correctly%20reproduces%20the%20seasonal%20temperature%20variations%20that%20drive%20the%20lake%20stratification%20and%20impact%20the%20vertical%20distributions%20of%20phytoplankton.%20Our%20model%20was%20able%20to%20replicate%20the%20space%5Cu2013time%20dynamics%20of%20the%20March%5Cu2013April%202015%20algal%20bloom%20similarly%20to%20what%20was%20observed%20on%20satellite%20imagery.%20We%20believe%20that%20our%20multiscale%20ecohydrodynamic%20model%20is%20a%20promising%20tool%20to%20complement%20field%20observations%20and%20hence%20support%20water%20management%20in%20the%20lake%20and%20its%20watershed.%22%2C%22date%22%3A%2201%5C%2F2021%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ecolmodel.2020.109418%22%2C%22ISSN%22%3A%2203043800%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0304380020304750%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222020-12-29T06%3A27%3A02Z%22%7D%7D%2C%7B%22key%22%3A%22LIWXWBJ8%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Delandmeter%20et%20al.%22%2C%22parsedDate%22%3A%222018-03-29%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EDelandmeter%2C%20P.%2C%20Lambrechts%2C%20J.%2C%20Legat%2C%20V.%2C%20Vallaeys%2C%20V.%2C%20Naithani%2C%20J.%2C%20Thiery%2C%20W.%2C%20Remacle%2C%20J.-F.%2C%20%26amp%3B%20Deleersnijder%2C%20E.%20%282018%29.%20A%20fully%20consistent%20and%20conservative%20vertically%20adaptive%20coordinate%20system%20for%20SLIM%203D%20v0.4%20with%20an%20application%20to%20the%20thermocline%20oscillations%20of%20Lake%20Tanganyika.%20%3Ci%3EGeoscientific%20Model%20Development%3C%5C%2Fi%3E%2C%20%3Ci%3E11%3C%5C%2Fi%3E%283%29%2C%201161%26%23x2013%3B1179.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.5194%5C%2Fgmd-11-1161-2018%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.5194%5C%2Fgmd-11-1161-2018%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20fully%20consistent%20and%20conservative%20vertically%20adaptive%20coordinate%20system%20for%20SLIM%203D%20v0.4%20with%20an%20application%20to%20the%20thermocline%20oscillations%20of%20Lake%20Tanganyika%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Philippe%22%2C%22lastName%22%3A%22Delandmeter%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Valentin%22%2C%22lastName%22%3A%22Vallaeys%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jaya%22%2C%22lastName%22%3A%22Naithani%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Wim%22%2C%22lastName%22%3A%22Thiery%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jean-Fran%5Cu00e7ois%22%2C%22lastName%22%3A%22Remacle%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22The%20discontinuous%20Galerkin%20%28DG%29%20%5Cufb01nite%20element%20method%20is%20well%20suited%20for%20the%20modelling%2C%20with%20a%20relatively%20small%20number%20of%20elements%2C%20of%20three-dimensional%20%5Cufb02ows%20exhibiting%20strong%20velocity%20or%20density%20gradients.%20Its%20performance%20can%20be%20highly%20enhanced%20by%20having%20recourse%20to%20r-adaptivity.%20Here%2C%20a%20vertical%20adaptive%20mesh%20method%20is%20developed%20for%20DG%20%5Cufb01nite%20elements.%20This%20method%2C%20originally%20designed%20for%20%5Cufb01nite%20difference%20schemes%2C%20is%20based%20on%20the%20vertical%20diffusion%20of%20the%20mesh%20nodes%2C%20with%20the%20diffusivity%20controlled%20by%20the%20density%20jumps%20at%20the%20mesh%20element%20interfaces.%22%2C%22date%22%3A%222018-03-29%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.5194%5C%2Fgmd-11-1161-2018%22%2C%22ISSN%22%3A%221991-9603%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Fwww.geosci-model-dev.net%5C%2F11%5C%2F1161%5C%2F2018%5C%2F%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A51%3A08Z%22%7D%7D%2C%7B%22key%22%3A%22KG9W9LF3%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Vallaeys%20et%20al.%22%2C%22parsedDate%22%3A%222018%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EVallaeys%2C%20V.%2C%20K%26%23xE4%3Brn%26%23xE4%3B%2C%20T.%2C%20Delandmeter%2C%20P.%2C%20Lambrechts%2C%20J.%2C%20Baptista%2C%20A.%20M.%2C%20Deleersnijder%2C%20E.%2C%20%26amp%3B%20Hanert%2C%20E.%20%282018%29.%20Discontinuous%20Galerkin%20modeling%20of%20the%20Columbia%20River%26%23x2019%3Bs%20coupled%20estuary-plume%20dynamics.%20%3Ci%3EOcean%20Modelling%3C%5C%2Fi%3E%2C%20%3Ci%3E124%3C%5C%2Fi%3E%2C%20111%26%23x2013%3B124.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2018.02.004%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2018.02.004%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Discontinuous%20Galerkin%20modeling%20of%20the%20Columbia%20River%5Cu2019s%20coupled%20estuary-plume%20dynamics%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Valentin%22%2C%22lastName%22%3A%22Vallaeys%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Tuomas%22%2C%22lastName%22%3A%22K%5Cu00e4rn%5Cu00e4%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Philippe%22%2C%22lastName%22%3A%22Delandmeter%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Ant%5Cu00f3nio%20M.%22%2C%22lastName%22%3A%22Baptista%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Emmanuel%22%2C%22lastName%22%3A%22Hanert%22%7D%5D%2C%22abstractNote%22%3A%22The%20Columbia%20River%20%28CR%29%20estuary%20is%20characterized%20by%20high%20river%20discharge%20and%20strong%20tides%20that%20generate%20high%20velocity%20%5Cufb02ows%20and%20sharp%20density%20gradients.%20Its%20dynamics%20strongly%20a%5Cufb00ects%20the%20coastal%20ocean%20circulation.%20Tidal%20straining%20in%20turn%20modulates%20the%20strati%5Cufb01cation%20in%20the%20estuary.%20Simulating%20the%20hydrodynamics%20of%20the%20CR%20estuary%20and%20plume%20therefore%20requires%20a%20multi-scale%20model%20as%20both%20shelf%20and%20estuarine%20circulations%20are%20coupled.%20Such%20a%20model%20has%20to%20keep%20numerical%20dissipation%20as%20low%20as%20possible%20in%20order%20to%20correctly%20represent%20the%20plume%20propagation%20and%20the%20salinity%20intrusion%20in%20the%20estuary.%20Here%2C%20we%20show%20that%20the%203D%20baroclinic%20discontinuous%20Galerkin%20%5Cufb01nite%20element%20model%20SLIM%203D%20is%20able%20to%20reproduce%20the%20main%20features%20of%20the%20CR%20estuary-to-ocean%20continuum.%20We%20introduce%20new%20vertical%20discretization%20and%20mode%20splitting%20that%20allow%20us%20to%20model%20a%20region%20characterized%20by%20complex%20bathymetry%20and%20sharp%20density%20and%20velocity%20gradients.%20Our%20model%20takes%20into%20account%20the%20major%20forcings%2C%20i.e.%20tides%2C%20surface%20wind%20stress%20and%20river%20discharge%2C%20on%20a%20single%20multi-scale%20grid.%20The%20simulation%20period%20covers%20the%20end%20of%20spring-early%20summer%20of%202006%2C%20a%20period%20of%20high%20river%20%5Cufb02ow%20and%20strong%20changes%20in%20the%20wind%20regime.%20SLIM%203D%20is%20validated%20with%20insitu%20data%20on%20the%20shelf%20and%20at%20multiple%20locations%20in%20the%20estuary%20and%20compared%20with%20an%20operational%20implementation%20of%20SELFE.%20The%20model%20skill%20in%20the%20estuary%20and%20on%20the%20shelf%20indicate%20that%20SLIM%203D%20is%20able%20to%20reproduce%20the%20key%20processes%20driving%20the%20river%20plume%20dynamics%2C%20such%20as%20the%20occurrence%20of%20bidirectional%20plumes%20or%20reversals%20of%20the%20inner%20shelf%20coastal%20currents.%22%2C%22date%22%3A%2204%5C%2F2018%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ocemod.2018.02.004%22%2C%22ISSN%22%3A%2214635003%22%2C%22url%22%3A%22https%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS1463500318300507%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A57%3A29Z%22%7D%7D%2C%7B%22key%22%3A%22W9LQCTJP%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Delandmeter%20et%20al.%22%2C%22parsedDate%22%3A%222015%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EDelandmeter%2C%20P.%2C%20Lewis%2C%20S.%20E.%2C%20Lambrechts%2C%20J.%2C%20Deleersnijder%2C%20E.%2C%20Legat%2C%20V.%2C%20%26amp%3B%20Wolanski%2C%20E.%20%282015%29.%20The%20transport%20and%20fate%20of%20riverine%20fine%20sediment%20exported%20to%20a%20semi-open%20system.%20%3Ci%3EEstuarine%2C%20Coastal%20and%20Shelf%20Science%3C%5C%2Fi%3E%2C%20%3Ci%3E167%3C%5C%2Fi%3E%2C%20336%26%23x2013%3B346.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecss.2015.10.011%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecss.2015.10.011%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22The%20transport%20and%20fate%20of%20riverine%20fine%20sediment%20exported%20to%20a%20semi-open%20system%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Philippe%22%2C%22lastName%22%3A%22Delandmeter%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Stephen%20E.%22%2C%22lastName%22%3A%22Lewis%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Wolanski%22%7D%5D%2C%22abstractNote%22%3A%22Understanding%20the%20transport%20and%20fate%20of%20suspended%20sediment%20exported%20by%20rivers%20is%20crucial%20for%20the%20management%20of%20sensitive%20marine%20ecosystems.%20Sediment%20transport%20and%20fate%20can%20vary%20considerably%20depending%20on%20the%20geophysical%20characteristics%20of%20the%20coastal%20environment.%20Fine%20sediment%20transport%20was%20studied%20in%20a%20setting%20in%20between%20%5Cu201copen%5Cu201d%20%28uninterrupted%20coasts%29%20and%20%5Cu201csemi-enclosed%5Cu201d%20%28bays%29%20coastal%20systems%2C%20namely%20a%20%5Cu201csemi-open%5Cu201d%20system%20of%20shallow%20coastal%20water%20with%20long%20%28~20%20km%29%20stretches%20of%20open%20coasts%20separated%20by%20capes%20and%20headlands.%20The%20case%20study%20was%20the%20large%2C%20seasonal%2C%20Burdekin%20River%20that%20discharges%20to%20a%20wide%20continental%20shelf%20containing%20headlands%20and%20shallow%20embayments%20adjacent%20to%20the%20Great%20Barrier%20Reef%2C%20Australia.%20A%20new%20three-dimensional%20%5Cufb01ne%20sediment%20module%20for%20the%20unstructured-mesh%20SLIM%203D%20hydrodynamic%20model%20was%20developed.%20The%20model%20was%20successfully%20validated%20against%20available%20%5Cufb01eld%20data.%20The%20results%20were%20compared%20to%20previous%20studies%20on%20the%20Burdekin%20River%20sediment%20transport%20and%20differences%20were%20analysed.%20Wind%20direction%20and%20speed%20during%20river%20%5Cufb02oods%20largely%20control%20the%20dynamics%20and%20the%20fate%20of%20the%20%5Cufb01ne%20sediment.%20Most%20%2867%25%20for%202007%29%20of%20the%20riverine%20%5Cufb01ne%20sediment%20load%20is%20deposited%20near%20the%20river%20mouth%3B%20the%20remaining%20sediment%20is%20transported%20further%20a%5Cufb01eld%20in%20a%20riverine%20freshwater%20plume%3B%20that%20sediment%20can%20reach%20sensitive%20marine%20ecosystems%20and%20should%20be%20a%20priority%20for%20management.%20During%20the%20rest%20of%20the%20year%2C%20when%20the%20river%20%5Cufb02ow%20has%20ceased%2C%20wind-driven%20resuspension%20events%20redistribute%20the%20deposited%20sediment%20within%20embayments%20but%20generate%20negligible%20longshore%20transport.%20This%20study%20suggests%20that%20semi-open%20systems%20trap%20most%20of%20the%20riverine%20%5Cufb01ne%20sediment%2C%20somewhat%20like%20semi-enclosed%20systems.%22%2C%22date%22%3A%2212%5C%2F2015%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ecss.2015.10.011%22%2C%22ISSN%22%3A%2202727714%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0272771415301013%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T10%3A09%3A08Z%22%7D%7D%2C%7B%22key%22%3A%226Q2MYI33%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22K%5Cu00e4rn%5Cu00e4%20et%20al.%22%2C%22parsedDate%22%3A%222013%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EK%26%23xE4%3Brn%26%23xE4%3B%2C%20T.%2C%20Legat%2C%20V.%2C%20%26amp%3B%20Deleersnijder%2C%20E.%20%282013%29.%20A%20baroclinic%20discontinuous%20Galerkin%20finite%20element%20model%20for%20coastal%20flows.%20%3Ci%3EOcean%20Modelling%3C%5C%2Fi%3E%2C%20%3Ci%3E61%3C%5C%2Fi%3E%2C%201%26%23x2013%3B20.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2012.09.009%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2012.09.009%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20baroclinic%20discontinuous%20Galerkin%20finite%20element%20model%20for%20coastal%20flows%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Tuomas%22%2C%22lastName%22%3A%22K%5Cu00e4rn%5Cu00e4%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22Numerical%20modelling%20of%20coastal%20%5Cufb02ows%20is%20a%20challenging%20topic%20due%20to%20complex%20topography%20of%20the%20coastal%20zone%2C%20rapid%20%5Cufb02ow%20dynamics%20and%20large%20density%20variations.%20Such%20phenomena%20are%20best%20simulated%20with%20unstructured%20grid%20models%20due%20to%20their%20highly%20%5Cufb02exible%20spatial%20discretisation.%20This%20article%20presents%20a%20three-dimensional%20discontinuous%20Galerkin%20%5Cufb01nite%20element%20marine%20model.%20Discontinuous%20Galerkin%20spatial%20discretisation%20is%20combined%20with%20an%20explicit%20mode%20splitting%20time%20integration%20scheme.%20Slope%20limiters%20are%20introduced%20to%20guarantee%20high%20quality%20of%20the%20tracer%20%5Cufb01elds%20in%20the%20presence%20of%20strong%20gradients.%20Free%20surface%20movement%20is%20accounted%20for%20by%20means%20of%20an%20Arbitrary%20Lagrangian%20Eulerian%20%28ALE%29%20moving%20mesh%20method.%20Water%20volume%20and%20tracers%20are%20conserved.%20The%20conservation%20properties%20and%20baroclinic%20adjustment%20under%20gravity%20are%20tested%20with%20numerical%20benchmarks.%20Finally%2C%20the%20model%20is%20applied%20to%20the%20Rhine%20river%20plume%20in%20an%20idealised%20setting.%22%2C%22date%22%3A%2201%5C%2F2013%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ocemod.2012.09.009%22%2C%22ISSN%22%3A%2214635003%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS1463500312001333%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A54%3A20Z%22%7D%7D%2C%7B%22key%22%3A%22DA4A5GCX%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22K%5Cu00e4rn%5Cu00e4%20et%20al.%22%2C%22parsedDate%22%3A%222012%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EK%26%23xE4%3Brn%26%23xE4%3B%2C%20T.%2C%20Legat%2C%20V.%2C%20Deleersnijder%2C%20E.%2C%20%26amp%3B%20Burchard%2C%20H.%20%282012%29.%20Coupling%20of%20a%20discontinuous%20Galerkin%20finite%20element%20marine%20model%20with%20a%20finite%20difference%20turbulence%20closure%20model.%20%3Ci%3EOcean%20Modelling%3C%5C%2Fi%3E%2C%20%3Ci%3E47%3C%5C%2Fi%3E%2C%2055%26%23x2013%3B64.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2012.01.001%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2012.01.001%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Coupling%20of%20a%20discontinuous%20Galerkin%20finite%20element%20marine%20model%20with%20a%20finite%20difference%20turbulence%20closure%20model%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Tuomas%22%2C%22lastName%22%3A%22K%5Cu00e4rn%5Cu00e4%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Hans%22%2C%22lastName%22%3A%22Burchard%22%7D%5D%2C%22abstractNote%22%3A%22This%20paper%20describes%20an%20online%20coupling%20between%20a%203D%20discontinuous%20Galerkin%20%5Cufb01nite%20element%20marine%20model%20and%20a%201D%20vertical%20turbulence%20closure%20model%20based%20on%20%5Cufb01nite%20differences.%20The%20coupling%20exploits%20the%20topology%20of%20the%203D%20mesh%2C%20that%20is%20formed%20by%20stacking%20layers%20of%20prisms%20in%20the%20vertical%20direction.%20A%20robust%20mapping%20between%20the%20%5Cufb01nite%20difference%20grid%20and%20the%20%5Cufb01nite%20element%20function%20space%20is%20designed%2C%20taking%20into%20account%20the%20discontinuities%20in%20the%20latter.%20The%20coupling%20is%20tested%20with%20two%20horizontally%20homogeneous%20%5Cufb02ows%20and%20an%20idealised%203D%20estuary%20simulation.%20The%20results%20are%20in%20good%20agreement%20with%20those%20obtained%20with%20a%20%5Cufb01nite%20difference%20model%20using%20the%20same%20turbulence%20closure%2C%20indicating%20that%20the%20coupling%20does%20not%20deteriorate%20the%20performance%20of%20the%20turbulence%20model.%22%2C%22date%22%3A%221%5C%2F2012%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ocemod.2012.01.001%22%2C%22ISSN%22%3A%2214635003%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS1463500312000029%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A54%3A11Z%22%7D%7D%2C%7B%22key%22%3A%22WLI4YG9J%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Comblen%20et%20al.%22%2C%22parsedDate%22%3A%222010%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EComblen%2C%20R.%2C%20Blaise%2C%20S.%2C%20Legat%2C%20V.%2C%20Remacle%2C%20J.-F.%2C%20Deleersnijder%2C%20E.%2C%20%26amp%3B%20Lambrechts%2C%20J.%20%282010%29.%20A%20discontinuous%20finite%20element%20baroclinic%20marine%20model%20on%20unstructured%20prismatic%20meshes%3A%20Part%20II%3A%20implicit%5C%2Fexplicit%20time%20discretization.%20%3Ci%3EOcean%20Dynamics%3C%5C%2Fi%3E%2C%20%3Ci%3E60%3C%5C%2Fi%3E%286%29%2C%201395%26%23x2013%3B1414.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-010-0357-4%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-010-0357-4%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20discontinuous%20finite%20element%20baroclinic%20marine%20model%20on%20unstructured%20prismatic%20meshes%3A%20Part%20II%3A%20implicit%5C%2Fexplicit%20time%20discretization%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%22%2C%22lastName%22%3A%22Comblen%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22S%5Cu00e9bastien%22%2C%22lastName%22%3A%22Blaise%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jean-Fran%5Cu00e7ois%22%2C%22lastName%22%3A%22Remacle%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%2212%5C%2F2010%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs10236-010-0357-4%22%2C%22ISSN%22%3A%221616-7341%2C%201616-7228%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs10236-010-0357-4%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A48%3A32Z%22%7D%7D%2C%7B%22key%22%3A%22YT2QEMYI%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Blaise%20et%20al.%22%2C%22parsedDate%22%3A%222010%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EBlaise%2C%20S.%2C%20Comblen%2C%20R.%2C%20Legat%2C%20V.%2C%20Remacle%2C%20J.-F.%2C%20Deleersnijder%2C%20E.%2C%20%26amp%3B%20Lambrechts%2C%20J.%20%282010%29.%20A%20discontinuous%20finite%20element%20baroclinic%20marine%20model%20on%20unstructured%20prismatic%20meshes%3A%20Part%20I%3A%20space%20discretization.%20%3Ci%3EOcean%20Dynamics%3C%5C%2Fi%3E%2C%20%3Ci%3E60%3C%5C%2Fi%3E%286%29%2C%201371%26%23x2013%3B1393.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-010-0358-3%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1007%5C%2Fs10236-010-0358-3%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20discontinuous%20finite%20element%20baroclinic%20marine%20model%20on%20unstructured%20prismatic%20meshes%3A%20Part%20I%3A%20space%20discretization%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22S%5Cu00e9bastien%22%2C%22lastName%22%3A%22Blaise%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Richard%22%2C%22lastName%22%3A%22Comblen%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jean-Fran%5Cu00e7ois%22%2C%22lastName%22%3A%22Remacle%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Jonathan%22%2C%22lastName%22%3A%22Lambrechts%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%2212%5C%2F2010%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1007%5C%2Fs10236-010-0358-3%22%2C%22ISSN%22%3A%221616-7341%2C%201616-7228%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flink.springer.com%5C%2F10.1007%5C%2Fs10236-010-0358-3%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A47%3A59Z%22%7D%7D%2C%7B%22key%22%3A%22AVEPBCBL%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22White%20et%20al.%22%2C%22parsedDate%22%3A%222008%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EWhite%2C%20L.%2C%20Legat%2C%20V.%2C%20%26amp%3B%20Deleersnijder%2C%20E.%20%282008%29.%20Tracer%20Conservation%20for%20Three-Dimensional%2C%20Finite-Element%2C%20Free-Surface%2C%20Ocean%20Modeling%20on%20Moving%20Prismatic%20Meshes.%20%3Ci%3EMonthly%20Weather%20Review%3C%5C%2Fi%3E%2C%20%3Ci%3E136%3C%5C%2Fi%3E%282%29%2C%20420%26%23x2013%3B442.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1175%5C%2F2007MWR2137.1%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1175%5C%2F2007MWR2137.1%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Tracer%20Conservation%20for%20Three-Dimensional%2C%20Finite-Element%2C%20Free-Surface%2C%20Ocean%20Modeling%20on%20Moving%20Prismatic%20Meshes%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Laurent%22%2C%22lastName%22%3A%22White%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22Large-scale%20free-surface%20ocean%20models%20designed%20to%20run%20over%20climatic%20time%20scales%20are%20required%20to%20globally%20conserve%20the%20volume%20and%20any%20tracer%20up%20to%20machine%20precision.%20In%20addition%2C%20local%20consistency%20is%20critical%20and%20requires%20that%20the%20discrete%20tracer%20equation%20preserve%20constants%20in%20a%20closed%20domain%20and%20if%20there%20is%20no%20tracer%20source%20or%20sink.%20Local%20consistency%2C%20together%20with%20monotonicity%2C%20will%20ensure%20that%20no%20spurious%20tracer%20extrema%20occur.%20A%20three-dimensional%2C%20finite-element%2C%20shallow-water%20model%20is%20presented.%20The%20mesh%20is%20unstructured%20in%20the%20horizontal%2C%20extruded%20in%20the%20third%20dimension%2C%20and%20made%20up%20of%20multiple%20layers%20of%20prisms.%20In%20addition%2C%20the%20mesh%20is%20allowed%20to%20move%20in%20the%20vertical%20and%20adapts%20itself%20to%20the%20free-surface%20motions.%20It%20is%20shown%20that%20achieving%20consistency%20requires%20a%20discrete%20compatibility%20between%20the%20tracer%20and%20continuity%20equations.%20In%20addition%2C%20to%20ensure%20global%20tracer%20conservation%20in%20a%20consistent%20way%2C%20a%20discrete%20compatibility%20between%20the%20tracer%2C%20continuity%2C%20and%20free-surface%20elevation%20equations%20must%20be%20fulfilled.%20It%20is%20suggested%20that%20this%20compatibility%20constraint%2C%20together%20with%20the%20use%20of%20a%20numerically%20stable%20scheme%2C%20severely%20restricts%20the%20choice%20of%20usable%20finite-element%20spatial%20discretizations.%20A%20consistent%20and%20conservative%20time-stepping%20algorithm%20is%20described%20for%20which%20a%20unique%20time%20step%20is%20used.%20It%20is%20suggested%20that%20future%20research%20is%20needed%20in%20order%20to%20design%20a%20consistent%20and%20conservative%20split-explicit%20algorithm.%20Some%20illustrative%20test%20cases%20are%20presented%20in%20which%20the%20method%20is%20shown%20to%20satisfy%20all%20conservation%20properties.%20A%20few%20experiments%20in%20which%20consistency%20breaks%20down%20are%20carried%20out%2C%20and%20the%20consequences%20of%20this%20breakdown%20process%20are%20investigated.%22%2C%22date%22%3A%2202%5C%2F2008%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1175%5C%2F2007MWR2137.1%22%2C%22ISSN%22%3A%220027-0644%2C%201520-0493%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Fjournals.ametsoc.org%5C%2Fdoi%5C%2Fabs%5C%2F10.1175%5C%2F2007MWR2137.1%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A58%3A28Z%22%7D%7D%2C%7B%22key%22%3A%22PQ3F9YNL%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22White%20et%20al.%22%2C%22parsedDate%22%3A%222008%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EWhite%2C%20L.%2C%20Deleersnijder%2C%20E.%2C%20%26amp%3B%20Legat%2C%20V.%20%282008%29.%20A%20three-dimensional%20unstructured%20mesh%20finite%20element%20shallow-water%20model%2C%20with%20application%20to%20the%20flows%20around%20an%20island%20and%20in%20a%20wind-driven%2C%20elongated%20basin.%20%3Ci%3EOcean%20Modelling%3C%5C%2Fi%3E%2C%20%3Ci%3E22%3C%5C%2Fi%3E%281%26%23x2013%3B2%29%2C%2026%26%23x2013%3B47.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2008.01.001%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ocemod.2008.01.001%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22A%20three-dimensional%20unstructured%20mesh%20finite%20element%20shallow-water%20model%2C%20with%20application%20to%20the%20flows%20around%20an%20island%20and%20in%20a%20wind-driven%2C%20elongated%20basin%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Laurent%22%2C%22lastName%22%3A%22White%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Vincent%22%2C%22lastName%22%3A%22Legat%22%7D%5D%2C%22abstractNote%22%3A%22We%20present%20a%20new%20three-dimensional%2C%20unstructured%20mesh%20%5Cufb01nite%20element%20shallow-water%20model.%20The%20current%20con%5Cufb01guration%20is%20suitable%20for%20studying%20unstrati%5Cufb01ed%20%5Cufb02ows%20and%20the%20evolution%20of%20passive%20tracers.%20The%20model%20has%20a%20free%20surface%20and%20is%20hydrostatic.%20The%20mesh%20is%20unstructured%20in%20the%20horizontal%20and%20extruded%20towards%20the%20seabed%20in%20the%20direction%20parallel%20to%20the%20local%20gravity%20vector%20to%20generate%20a%20mesh%20made%20up%20of%20prisms.%20The%20mesh%20moves%20in%20the%20vertical%20and%20accommodates%20the%20free-surface%20motions.%20We%20describe%20the%20numerical%20treatment%20of%20the%20hydrodynamical%20equations%20with%20the%20%5Cufb01nite%20element%20method.%20A%20discontinuous%20representation%20is%20used%20in%20the%20vertical%20for%20all%20velocity%20components.%20The%20horizontal%20velocity%20components%20are%20non-conforming%20in%20the%20horizontal%2C%20which%20is%20particularly%20appropriate%20for%20advection-dominated%20%5Cufb02ows.%20The%20model%20is%20validated%20against%20a%20realistic%20tidal%20%5Cufb02ow%20around%20a%20shallow-water%20island%20for%20which%20%5Cufb01eld%20measurements%20are%20available%20and%20is%20shown%20to%20operate%20successfully.%20The%20three-dimensional%20character%20of%20the%20%5Cufb02ow%20is%20emphasized%20by%20use%20of%20a%20passive%20tracer.%20We%20also%20assess%20the%20model%5Cu2019s%20ability%20to%20represent%20the%20vertical%20structure%20of%20the%20horizontal%20%5Cufb02ow%20%5Cufb01eld%20by%20applying%20it%20to%20a%20wind-driven%20%5Cufb02ow%20experiment%20in%20an%20elongated%20rectangular%20basin.%22%2C%22date%22%3A%221%5C%2F2008%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ocemod.2008.01.001%22%2C%22ISSN%22%3A%2214635003%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS1463500308000140%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A58%3A12Z%22%7D%7D%2C%7B%22key%22%3A%22LXLUG7Q8%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22White%20and%20Deleersnijder%22%2C%22parsedDate%22%3A%222007%22%2C%22numChildren%22%3A2%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3EWhite%2C%20L.%2C%20%26amp%3B%20Deleersnijder%2C%20E.%20%282007%29.%20Diagnoses%20of%20vertical%20transport%20in%20a%20three-dimensional%20finite%20element%20model%20of%20the%20tidal%20circulation%20around%20an%20island.%20%3Ci%3EEstuarine%2C%20Coastal%20and%20Shelf%20Science%3C%5C%2Fi%3E%2C%20%3Ci%3E74%3C%5C%2Fi%3E%284%29%2C%20655%26%23x2013%3B669.%20%3Ca%20href%3D%27https%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecss.2006.07.014%27%3Ehttps%3A%5C%2F%5C%2Fdoi.org%5C%2F10.1016%5C%2Fj.ecss.2006.07.014%3C%5C%2Fa%3E%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22Diagnoses%20of%20vertical%20transport%20in%20a%20three-dimensional%20finite%20element%20model%20of%20the%20tidal%20circulation%20around%20an%20island%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Laurent%22%2C%22lastName%22%3A%22White%22%7D%2C%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Eric%22%2C%22lastName%22%3A%22Deleersnijder%22%7D%5D%2C%22abstractNote%22%3A%22A%20three-dimensional%20%5Cufb01nite%20element%20model%20is%20used%20to%20investigate%20the%20formation%20of%20shallow-water%20eddies%20in%20the%20wake%20of%20Rattray%20Island%20%28Great%20Barrier%20Reef%2C%20Australia%29.%20Field%20measurements%20and%20visual%20observations%20show%20that%20stable%20eddies%20develop%20in%20the%20lee%20of%20the%20island%20at%20rising%20and%20falling%20tides.%20The%20water%20turbidity%20downstream%20of%20the%20island%20suggests%20the%20existence%20of%20strong%20upwelling%20that%20would%20be%20responsible%20for%20carrying%20bed%20sediments%20up%20to%20the%20sea%20surface.%20We%20%5Cufb01rst%20propose%20to%20look%20at%20the%20upwelling%20velocity%20and%20then%20use%20the%20theory%20of%20the%20age%20to%20diagnose%20vertical%20transport.%20The%20water%20age%20is%20de%5Cufb01ned%20as%20the%20time%20elapsed%20since%20particles%20of%20water%20left%20the%20sea%20bottom%2C%20where%20the%20age%20is%20prescribed%20to%20be%20zero.%20Two%20versions%20of%20this%20diagnosis%20are%20considered.%20Although%20the%20model%20predicts%20upwelling%20within%20the%20eddies%2C%20it%20is%20not%20suf%5Cufb01ciently%20intense%20to%20account%20for%20vertical%20transport%20throughout%20the%20water%20column%20during%20the%20life%20span%20of%20the%20eddies.%20As%20mesh%20resolution%20increases%2C%20this%20upwelling%20does%20not%20intensify.%20However%2C%20strong%20upwelling%20is%20then%20resolved%20off%20the%20island%5Cu2019s%20tips%2C%20which%20is%20con%5Cufb01rmed%20by%20the%20results%20obtained%20with%20the%20age.%20This%20study%20also%20shows%20that%20the%20%5Cufb01nite%20element%20method%2C%20together%20with%20unstructured%20meshes%2C%20performs%20well%20for%20representing%20three-dimensional%20%5Cufb02ow%20past%20an%20island.%22%2C%22date%22%3A%229%5C%2F2007%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%2210.1016%5C%2Fj.ecss.2006.07.014%22%2C%22ISSN%22%3A%2202727714%22%2C%22url%22%3A%22http%3A%5C%2F%5C%2Flinkinghub.elsevier.com%5C%2Fretrieve%5C%2Fpii%5C%2FS0272771406003374%22%2C%22collections%22%3A%5B%22GJSQZPDC%22%5D%2C%22dateModified%22%3A%222018-10-21T09%3A58%3A00Z%22%7D%7D%2C%7B%22key%22%3A%22CY8VSC94%22%2C%22library%22%3A%7B%22id%22%3A778265%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22Sterckx%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3ESterckx%2C%20K.%20%28n.d.%29.%20The%20impact%20of%20seasonal%20variability%20and%20climate%20change%20on%20lake%20Tanganyika%26%23x2019%3Bs%20hydrodynamics.%20%3Ci%3EEnvironmental%20Fluid%20Mechanics%3C%5C%2Fi%3E.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22journalArticle%22%2C%22title%22%3A%22The%20impact%20of%20seasonal%20variability%20and%20climate%20change%20on%20lake%20Tanganyika%5Cu2019s%20hydrodynamics%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22Kevin%22%2C%22lastName%22%3A%22Sterckx%22%7D%5D%2C%22abstractNote%22%3A%22In%20this%20paper%2C%20we%20project%20future%20changes%20in%20the%20hydrodynamics%20of%20Lake%20Tanganyika%20under%20a%20high%20emission%20scenario%20using%20the%20three-dimensional%20%283D%29%20version%20of%20the%20Second-generation%20Louvain-la-Neuve%20Ice-ocean%20Model%20%28SLIM%203D%29%20forced%20by%20a%20high-resolution%20regional%20climate%20model.%20We%20demonstrate%20the%20advantages%20of%203D%20simulation%20compared%20to%201D%20vertical%20models.%20The%20model%20captures%20the%20seasonal%20variability%20in%20the%20lake%2C%20with%20seasonal%20deep%20mixing%20and%20surfacing%20of%20the%20thermocline.%20In%20a%20simulation%20of%20current%20conditions%2C%20the%20thermocline%20in%20the%20south%20of%20the%20lake%20moves%20upward%20from%20a%20depth%20of%2075%20m%20until%20it%20reaches%20the%20lake%20surface%20during%20August%20and%20September.%20We%20compare%20the%20current%20conditions%20with%20an%20end-of-the-century%20simulation%20under%20a%20pessimistic%20emission%20scenario%20%28RCP%208.5%29%20showing%20that%20surface%20water%20temperature%20increases%20on%20average%20by%203%5Cu2009%5Cu00b1%5Cu20090.5%20%5Cu00b0C.%20Because%20deeper%20water%20warms%20less%2C%20the%20stratification%20increases%20in%20the%20upper%20150%20m%20of%20the%20water%20column.%20This%20temperature-induced%20stratification%20reduces%20mixing%20and%20prevents%20the%20outcropping%20of%20the%20thermocline%2C%20eventually%20shutting%20down%20the%20ventilation%20of%20deep%20water%20in%20the%20south%20basin.%20Our%20results%20highlight%20the%20extreme%20changes%20likely%20faced%20by%20Lake%20Tanganyika%20if%20global%20greenhouse%20gas%20emissions%20are%20not%20curbed.%22%2C%22date%22%3A%22%22%2C%22language%22%3A%22en%22%2C%22DOI%22%3A%22%22%2C%22ISSN%22%3A%22%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222023-01-10T18%3A50%3A23Z%22%7D%7D%5D%7D
Sterckx, K., Delandmeter, P., Lambrechts, J., Deleersnijder, E., Verburg, P., & Thiery, W. (2023). The impact of seasonal variability and climate change on lake Tanganyika’s hydrodynamics.
Environmental Fluid Mechanics .
https://doi.org/10.1007/s10652-022-09908-8
Ishimwe, A. P., Deleersnijder, E., Legat, V., & Lambrechts, J. (2023). A split-explicit second order Runge–Kutta method for solving 3D hydrodynamic equations.
Ocean Modelling ,
186 , 102273.
https://doi.org/10.1016/j.ocemod.2023.102273
Alaerts, L., Dobbelaere, T., Gravinese, P. M., & Hanert, E. (2022). Climate Change Will Fragment Florida Stone Crab Communities.
Frontiers in Marine Science ,
9 , 839767.
https://doi.org/10.3389/fmars.2022.839767
Vallaeys, V., Lambrechts, J., Delandmeter, P., Pätsch, J., Spitzy, A., Hanert, E., & Deleersnijder, E. (2021). Understanding the circulation in the deep, micro-tidal and strongly stratified Congo River estuary.
Ocean Modelling , 101890.
https://doi.org/10.1016/j.ocemod.2021.101890
Duquesne, F., Vallaeys, V., Vidaurre, P. J., & Hanert, E. (2021). A coupled ecohydrodynamic model to predict algal blooms in Lake Titicaca.
Ecological Modelling ,
440 , 109418.
https://doi.org/10.1016/j.ecolmodel.2020.109418
Delandmeter, P., Lambrechts, J., Legat, V., Vallaeys, V., Naithani, J., Thiery, W., Remacle, J.-F., & Deleersnijder, E. (2018). A fully consistent and conservative vertically adaptive coordinate system for SLIM 3D v0.4 with an application to the thermocline oscillations of Lake Tanganyika.
Geoscientific Model Development ,
11 (3), 1161–1179.
https://doi.org/10.5194/gmd-11-1161-2018
Vallaeys, V., Kärnä, T., Delandmeter, P., Lambrechts, J., Baptista, A. M., Deleersnijder, E., & Hanert, E. (2018). Discontinuous Galerkin modeling of the Columbia River’s coupled estuary-plume dynamics.
Ocean Modelling ,
124 , 111–124.
https://doi.org/10.1016/j.ocemod.2018.02.004
Delandmeter, P., Lewis, S. E., Lambrechts, J., Deleersnijder, E., Legat, V., & Wolanski, E. (2015). The transport and fate of riverine fine sediment exported to a semi-open system.
Estuarine, Coastal and Shelf Science ,
167 , 336–346.
https://doi.org/10.1016/j.ecss.2015.10.011
Kärnä, T., Legat, V., & Deleersnijder, E. (2013). A baroclinic discontinuous Galerkin finite element model for coastal flows.
Ocean Modelling ,
61 , 1–20.
https://doi.org/10.1016/j.ocemod.2012.09.009
Kärnä, T., Legat, V., Deleersnijder, E., & Burchard, H. (2012). Coupling of a discontinuous Galerkin finite element marine model with a finite difference turbulence closure model.
Ocean Modelling ,
47 , 55–64.
https://doi.org/10.1016/j.ocemod.2012.01.001
Comblen, R., Blaise, S., Legat, V., Remacle, J.-F., Deleersnijder, E., & Lambrechts, J. (2010). A discontinuous finite element baroclinic marine model on unstructured prismatic meshes: Part II: implicit/explicit time discretization.
Ocean Dynamics ,
60 (6), 1395–1414.
https://doi.org/10.1007/s10236-010-0357-4
Blaise, S., Comblen, R., Legat, V., Remacle, J.-F., Deleersnijder, E., & Lambrechts, J. (2010). A discontinuous finite element baroclinic marine model on unstructured prismatic meshes: Part I: space discretization.
Ocean Dynamics ,
60 (6), 1371–1393.
https://doi.org/10.1007/s10236-010-0358-3
White, L., Legat, V., & Deleersnijder, E. (2008). Tracer Conservation for Three-Dimensional, Finite-Element, Free-Surface, Ocean Modeling on Moving Prismatic Meshes.
Monthly Weather Review ,
136 (2), 420–442.
https://doi.org/10.1175/2007MWR2137.1
White, L., Deleersnijder, E., & Legat, V. (2008). A three-dimensional unstructured mesh finite element shallow-water model, with application to the flows around an island and in a wind-driven, elongated basin.
Ocean Modelling ,
22 (1–2), 26–47.
https://doi.org/10.1016/j.ocemod.2008.01.001
White, L., & Deleersnijder, E. (2007). Diagnoses of vertical transport in a three-dimensional finite element model of the tidal circulation around an island.
Estuarine, Coastal and Shelf Science ,
74 (4), 655–669.
https://doi.org/10.1016/j.ecss.2006.07.014
Sterckx, K. (n.d.). The impact of seasonal variability and climate change on lake Tanganyika’s hydrodynamics. Environmental Fluid Mechanics .